深度神经网络基础层算子介绍
1. 卷积算子
基础概念
(1) 卷积核(Kernel)。图像处理时,对输入图像中一个小区域像素加权平均后成为输出图像的一种操作。
(2) 填充(Padding)。填充是指处理输入特征图(Feature Map)边界的方式。
(3) 步长(Stride)。步长即卷积核遍历输入特征图时每步移动的像素数。
(4) 输出特征图尺寸。有了上面三个概念,我们就可以定义卷积运算后输出特征图的尺寸大小了。
定义深度神经网络图像卷积输出特征图尺寸的计算公式为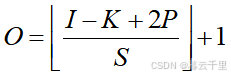
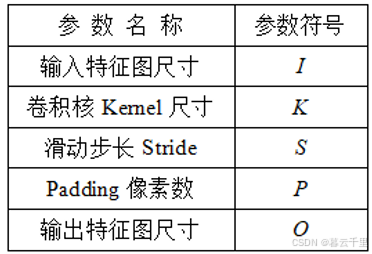
假设3 × 3数据矩阵P如图所示(我们常见的图像一般是三通道的,这里为方便理解,举个单通道的例子)。

首先对矩阵P进行Padding补0,将其扩充至5 × 5的P_padding,Padding = n,即在图片矩阵四周补n圈0(此处为方便起见,以Padding = 1为例,具体Padding值根据实际需求而定)。然后将P_padding与卷积核Kernel作卷积运算。已知输入特征图尺寸I = 3,卷积核Kernel尺寸K = 3,滑动步长S = 1,Padding像素数P = 1,则输出特征图尺寸为
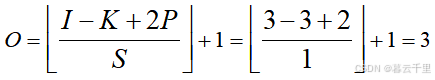
而实际应用中,会使用多个卷积核得到多个输出特征图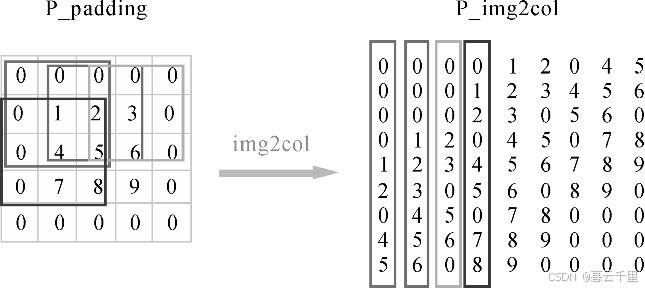
不同灰度框表示从输入特征图矩阵中依次提取出和卷积核一样大小的块数据。为了提高卷积操作的运算效率,需要进行img2col(图像矩阵转成列)操作,即把这些不同灰度框内的数据向量化。共有3 × 3个向量,最后得到9个向量化的数据矩阵。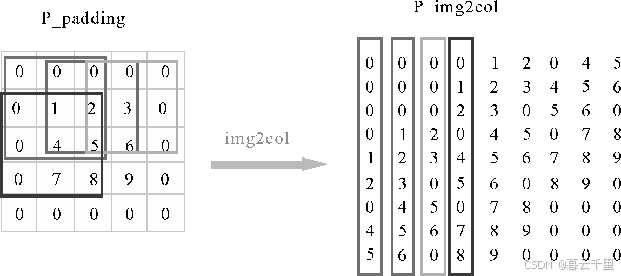
接着进行矩阵相乘操作,即将卷积核Kernel展成行,与图像矩阵展成的列进行矩阵相乘: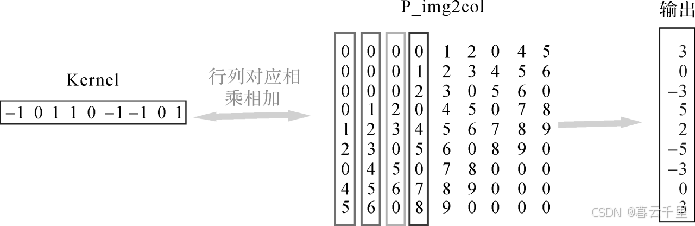
最后进行col2img(矩阵转特征图)操作,即将生成的列向量转成矩阵输出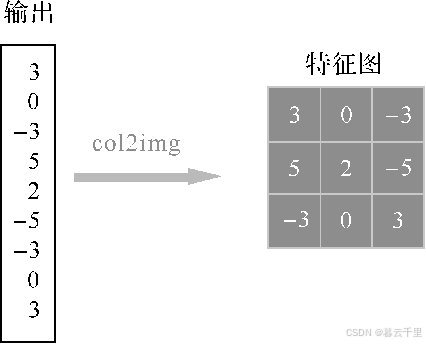
卷积运算示意图: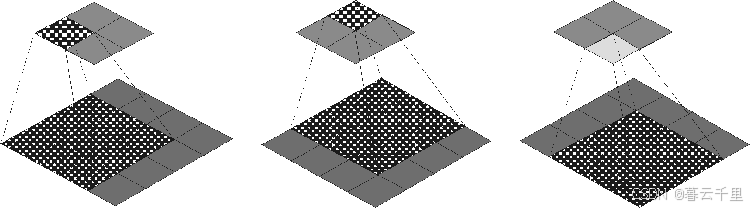
2. 反卷积算子
反卷积算子是一种上采样算子,常被应用于场景分割、生成模型等算法网络中。它有很多其他的叫法,如Transposed Convolution(转置卷积)、Fractional Strided Convolution(小步长卷积)等。
已知输入特征图尺寸I = 4,卷积核Kernel尺寸 K = 3,滑动步长S = 1,Padding像素数P = 0,则输出特征图尺寸为: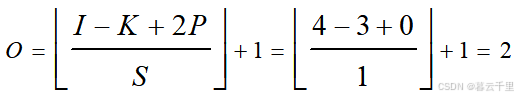
其对应的反卷积参数为(I′= 2,K′= 3,S′= 1,P′= 2,O′= 4)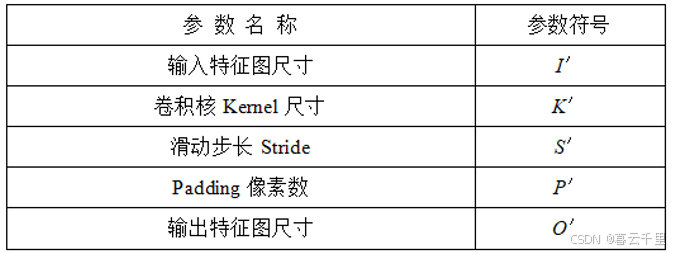
反卷积运算示意图: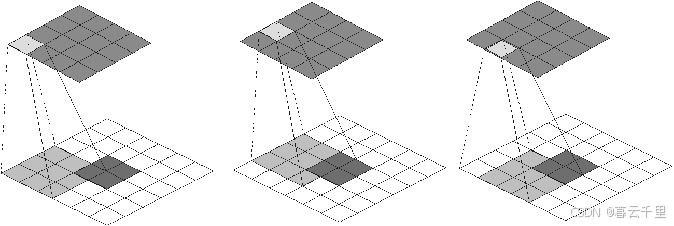
可以发现,卷积和反卷积操作中K = K′,S = S′,但是卷积的P = 0,反卷积的P′= 2通过对比可以发现,卷积层中左上角的输入只对左上角的输出有贡献,所以反卷积层会出现P′= K - P - 1 = 2。
通过示意图可以发现,反卷积层的输入/输出在S = S’ = 1时的关系为
O′= I′ - K′ + 2P′+ 1 = I′+ (K - 1) - 2P
3. 池化算子
常用的池化算子有:
(1) 平均池化算子:
进行池化操作时,对局部感受野中的所有值求均值并作为采样值。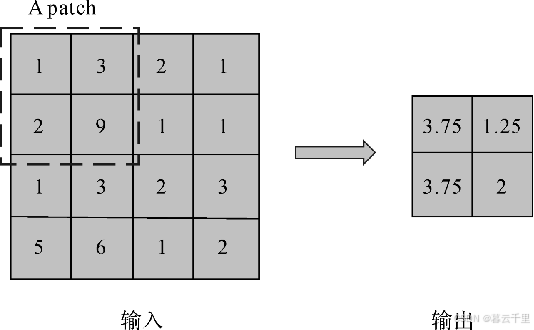
(2) 最大池化算子:
进行池化操作时,取局部感受野中的最大值作为采样值。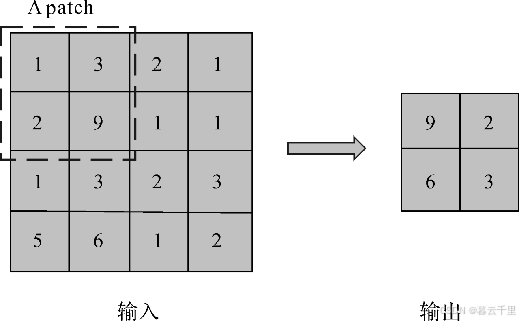
4. 激活算子
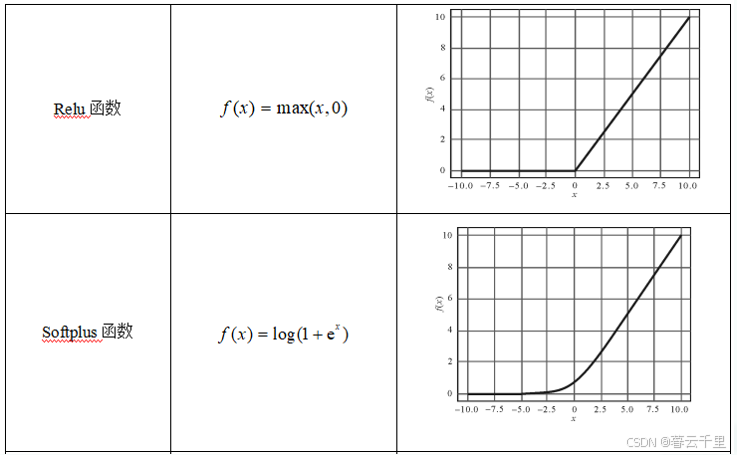
常用的激活函数有Sigmoid函数、Tanh函数、Relu函数、Softplus函数和Leaky_relu函数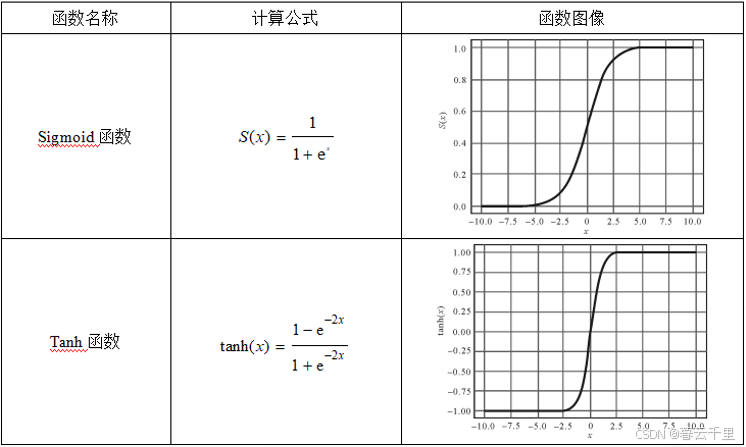
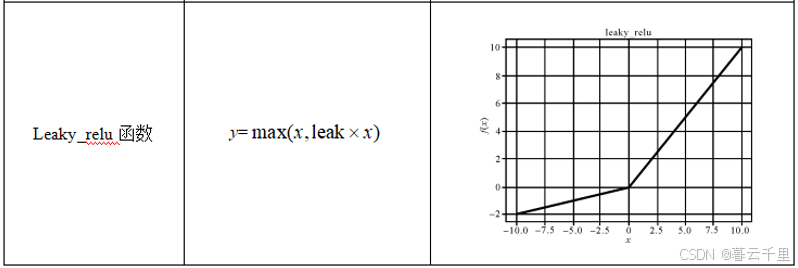
5. 全连接算子
下图为全连接层的过程。X是全连接层的输入,也就是特征;W是全连接层的参数,也称为权值。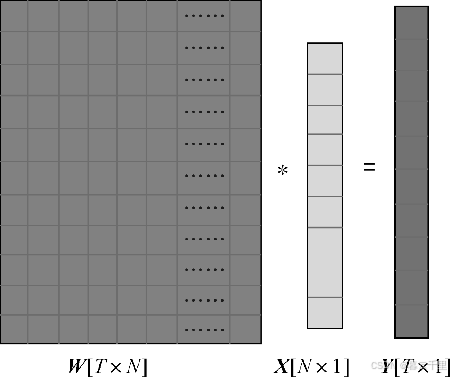
特征X是由全连接层前面多个卷积层和池化层处理后得到的。假设全连接层前面连接的是一个卷积层,这个卷积层输出了100个特征(也就是我们常说的特征图的通道为100),每个特征的大小是4 × 4,在将100个特征输入给全连接层之前Flatten层会将这些特征拉平成N行1列的一维向量,此时,N = 100 × 4 × 4 = 1600,则特征向量X为1600行1列的一维向量。
全连接层的参数W是深度神经网络训练过程中全连接层寻求的最优权值,可表示为T行N列的二维向量,其中T表示类别数。例如,需要解决的是7分类问题,则T = 7,其他分类数目以此类推。通过W × X = Y,得到T行1列的一维向量,即为全连接层的输出。
6. Softmax算子
Softmax算子用于多分类问题,是分类型神经网络中的输出层(Softmax层)函数,它可以计算出神经网络输出层的值。因此,Softmax算子主要作用于神经网络的最后一层,旨在输出输入样本属于各个类别的概率。
如图,全连接层的输出向量Y中的数字范围是( -∞,+∞),而Softmax层的作用是使输出向量Y中的数字在(0, 1)之间改变。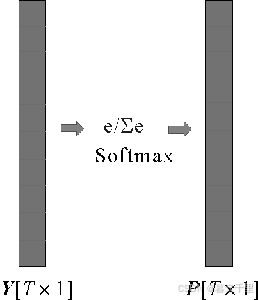
Softmax算子的计算公式为: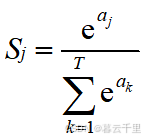
式中:aj、ak分别表示全连接层的输出向量Y的第j个和第k个值。
通过Softmax算子的计算后,得到输出向量P,P中的数值Sj∈(0,1),j∈[1,T ]。其中Sj 表示输入样本属于该j类别的概率,概率值越大,则输入样本属于该类别的可能性越大。实际中,可以利用Softmax算子解决样本的多分类问题。
7. 批标准化算子
同卷积层、池化层、全连接层、激活层一样,批标准化(Batch Normalization,又称批归一化)层也属于网络的一层。批标准化算子(后面简称BN算子)由谷歌于2015年提出,这是一个深度神经网络训练的技巧,它不仅可以加快模型的收敛速度,而且可以缓解深层网络中“梯度弥散”的问题,从而使得训练深层网络模型更加容易和稳定。
网络一旦训练起来,参数就需要更新,前面层训练参数的更新将导致后面层输入数据分布的变化,进而上层的网络需要不停地去适应这些分布变化,这使得模型训练变得困难。假设某个神经元输入为x,权重为W,输出y = f(Wx + b),激活函数f为Tanh函数(如图3-14所示)。当x在[-1, 1]之间变化时,输出随着输入变化,但是在此区间之外输出几乎没什么变化,即无论输入再怎么扩大,Tanh激活函数输出值仍接近1,也就是说,输出对比较大的输入值不敏感了。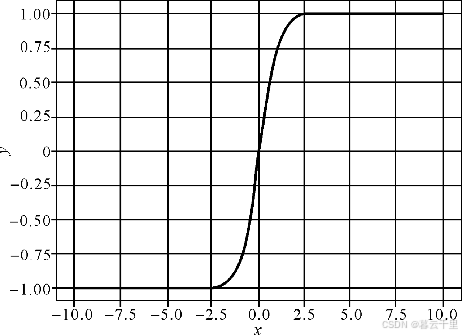
Tanh激活函数
BN算子的具体运算主要分为以下4步:
(1) 求每一个批次训练数据的均值μB,即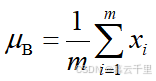
式中:xi为该批次的训练数据;m为该批次包含的训练数据的个数。
(2) 求每一个批次训练批数据的方差,即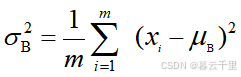
(3) 利用前两步求得的均值和方差,对该批次训练数据做标准化,获得标准化的输入,即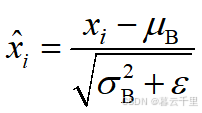
式中:ε是为了避免除数为0所使用的微小正数。
(4) 对标准化的输入 xi 进行尺度变换和偏移,得到对应层的输出yi,即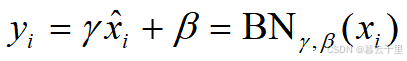
式中:γ是尺度因子;β是平移因子。这一步是BN的精髓。由于标准化后的xi基本会被限制在正态分布下,因此网络的表达能力下降。为解决该问题,我们引入两个新的参数:γ、β。γ和β是在训练时网络自己学习得到的。
8. Shortcut算子
Shortcut(“直连”或“捷径”)是CNN模型发展中出现的一种非常有效的结构。研究人员发现,网络的深度对CNN的效果影响非常大。理论上,网络的层数越多,能够提取到不同层次的特征越丰富,网络学习生成的模型预测的准确率就越高;但实际上,单纯地增加网络深度并不能提高网络的效果,反而会造成“梯度弥散”或“梯度爆炸”,损害模型的效果。
Highway(高速)是较早将Shortcut的思想引入深度模型中的一种方法。最初的CNN模型只有相邻两层之间存在连接,如图3-15所示,x、y是相邻两层,通过WH连接,多个这样的层前后串接起来就形成了深度网络。相邻层之间的关系为:
y = H(x, WH)
式中:H表示网络中的变换。
最初CNN相邻两层之间的连接:
为了解决深度网络中梯度弥散和退化的问题,Highway在两层之间增加了带权的Shortcut。两层之间的结构如图所示。
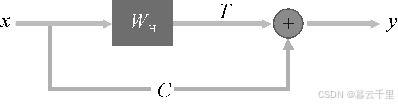
x与y的关系为: y = H(x, WH)·T(x, WT) + x·C(x, WC)
式中:T称为“transform gate”(传输门);C称为“carry gate”(搬运门)。输入层x通过C的加权连接到输出层y。这种连接方式的好处是,不管梯度怎么下降,总有C支路是直接累加上去的,它的梯度不会消失,从而缓解了深度网络中的梯度发散问题。另外,如果某一层是冗余的,我们只需要让该层学习到C支路为x,T支路为0,即输入是x,经过该冗余层后,输出仍然为x。这样当网络自行决定了哪些层为冗余层后,自然解决了退化问题。
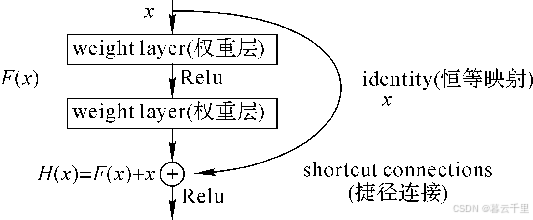
当然还有很多其他的利用Shortcut算子的网络模型,典型的如ResNet,它是Highway网络的一个特例。ResNet引入了残差网络结构,通过这种残差网络结构,可以把网络层设计得更深(目前可以达到1000多层),而且最终的分类效果也非常好。
残差网络的基本结构 :