阅读量:3
目录
如何衡量一个代码的好坏
- 算法效率分析分为两种
- 时间效率,称为时间复杂度,主要是用来衡量算法的运行速度
- 空间效率,称为空间复杂度,主要是用来衡量实现一个算法需要的额外空间
时间复杂度
概念
定义
- 算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间
- 一个算法所花费的时间与其语句中的执行次数成正比,算法中的基本操作的执行次数,为算法的时间复杂度
计算方法
void func1(int N){ int count = 0; for (int i = 0; i < N ; i++) { for (int j = 0; j < N ; j++) { count++; //————>N*N } } for (int k = 0; k < 2 * N ; k++) { count++; //————>N*2 } int M = 10; while ((M--) > 0) { count++; //————>10 } System.out.println(count); } Func1执行的基本操作次数为:
- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
推导大O阶方法(大O符号,用于描述函数渐进行为的数学符号)
- 用常数 1 取代运行时间中的所有加法常数
- 在修改后的运行次数函数中,只保留最高项
- 如果最高阶存在且不为 1,则去除与这个项相乘的常数
- 使用大O阶渐进表示法后,func的时间复杂度为:

实例计算
【实例1】
//计算func2的时间复杂度 void func2(int N) { int count = 0; for (int k = 0; k < 2 * N ; k++) { count++; //————>N*2 } int M = 10; while ((M--) > 0) { count++; //————>10 } System.out.println(count); } - func2的时间复杂度为:
 即
即 
【实例2】
//计算func3的时间复杂度 void func3(int N, int M) { int count = 0; for (int k = 0; k < M; k++) { count++; //————>M } for (int k = 0; k < N ; k++) { count++; //————>N } System.out.println(count); }
- func3的时间复杂度为:
【实例3】
// 计算func4的时间复杂度 void func4(int N) { int count = 0; for (int k = 0; k < 100; k++) { count++; //————>100 } System.out.println(count); }
- func4的时间复杂度为:
【实例4】:冒泡排序的时间复杂度
// 计算bubbleSort的时间复杂度 void bubbleSort(int[] array) { for (int end = array.length; end > 0; end--) { //————>(N-1)项 boolean sorted = true; for (int i = 1; i < end; i++) { //———>(N-1)+(N-2)+(N-3)+...+1 if (array[i - 1] > array[i]) { //等差数列求和,首:N-1 末:1 项数:N-1 Swap(array, i - 1, i); sorted = false; } } if (sorted == true) { break; } } }
- 第11,12行对代码进行了优化,时间复杂度为:
- 若无优化,最好和最坏的结果都是:
即
【实例5】:二分查找的时间复杂度
// 计算binarySearch的时间复杂度 int binarySearch(int[] array, int value) { int begin = 0; int end = array.length - 1; while (begin <= end) { int mid = begin + ((end-begin) / 2); if (array[mid] < value) begin = mid + 1; else if (array[mid] > value) end = mid - 1; else; return mid; } return -1; }
- 分一次,还剩
个数;分两次,还剩
个数......分
次,还剩
个数。
- 在结果最坏时,当只有一个剩余的数的时候,就找到了,所以此时
,即
- binarySearch的时间复杂度为:
【实例6】:阶乘递归的时间复杂度
// 计算阶乘递归factorial的时间复杂度 long factorial(int N) { return N < 2 ? N : factorial(N-1) * N; }
- 递归的复杂度 = 递归的次数 * 每次递归后代码的执行次数
- 递归的次数为N;每次递归回来执行三目运算,它的时间复杂度为
- 阶乘递归的时间复杂度为:
【实例7】:斐波那契递归的时间复杂度
// 计算斐波那契递归fibonacci的时间复杂度 int fibonacci(int N) { return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2); } 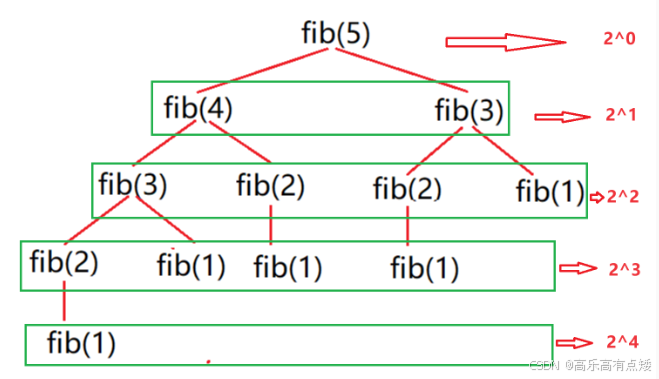
- 第 n 层节点个数为:
,则总递归次数为:
- 每次递归后代码执行三目运算,时间复杂度为:
- 斐波那契递归的时间复杂度为:
空间复杂度
概念
- 空间复杂度是对一个算法在运行过程中,临时占用存储空间大小的量度。
- 计算规则基本上与时间复杂度一样,也使用大O渐进法表示
实例计算
【实例1】:冒泡排序的空间复杂度
// 计算bubbleSort的空间复杂度 void bubbleSort(int[] array) { for (int end = array.length; end > 0; end--) { boolean sorted = true; for (int i = 1; i < end; i++) { if (array[i - 1] > array[i]) { Swap(array, i - 1, i); sorted = false; } } if (sorted == true) { break; } } }
- 空间复杂度为:
【实例2】:斐波那契的空间复杂度
// 计算fibonacci的空间复杂度 int[] fibonacci(int n) { long[] fibArray = new long[n + 1]; fibArray[0] = 0; fibArray[1] = 1; for (int i = 2; i <= n ; i++) { fibArray[i] = fibArray[i - 1] + fibArray [i - 2]; } return fibArray; }
- 空间复杂度为:
【实例3】:阶乘递归的空间复杂度
// 计算阶乘递归Factorial的空间复杂度 long factorial(int N) { return N < 2 ? N : factorial(N-1)*N; }
- 空间复杂度为:
