Floodfill,翻译为洪水灌溉,而floodfill算法本质上是为了解决在矩阵中性质相同的联通块问题。
一、图像渲染
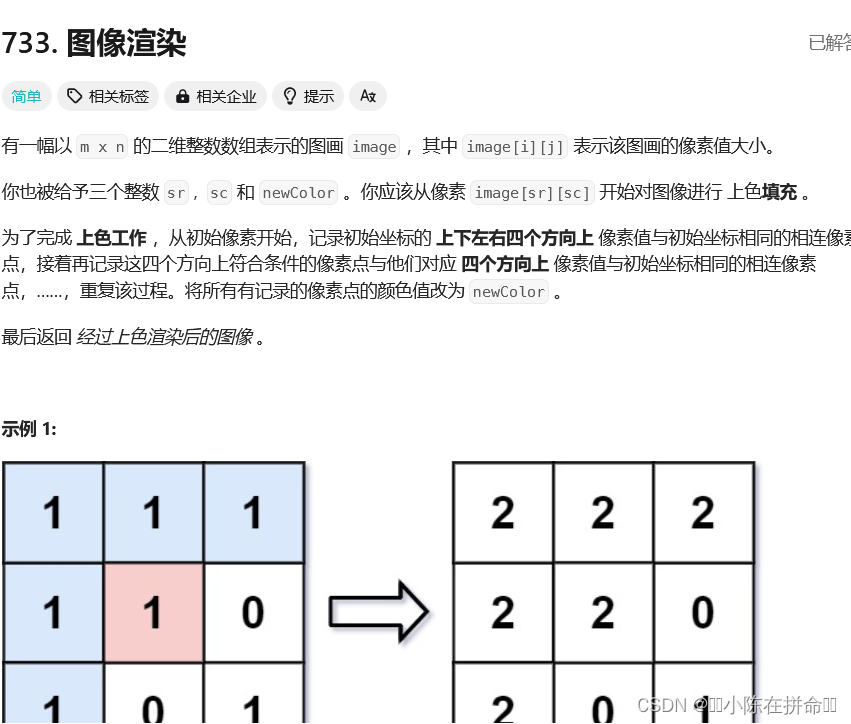
与dfs一样,从指定的起点开始向四个方向扩展,区别就是用之前通过参数将下标关系传递给dfs,而现在是将下标关系的键值对传给queue。
class Solution { public: //定义4个方向 int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; typedef pair<int,int> PII; vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) { //采用BFS算法解决floodfill算法, 解决相同性质的矩阵联通块问题 int prev=image[sr][sc]; if(prev==color) return image; int m=image.size(),n=image[0].size(); queue<PII> q;//队列 q.emplace(sr,sc); while(!q.empty()) { //先修改当前位置 auto [a,b]=q.front();//c++14的玩法 q.pop(); image[a][b]=color;//修改成color for(int k=0;k<4;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&& image[x][y]==prev) q.emplace(x,y); } } return image; } };二、岛屿数量

1. 因为要计算岛屿的数量,所以我们每进行一次bfs就要统计一下该岛屿,因为我们可以将bfs单独封装成一个函数。
2.在扩展的时候,我们需要标记我们扩展过的网格,这里有两种方案:
(1)修改值,但是修改值会改变原数据,必须要想办法修改回来。
(2)标记数组(常用),相同大小的标记数组,将探索过的网格标记为true
class Solution { public: int dx[4]={1,-1,0,0}; int dy[4]={0,0,1,-1}; typedef pair<int,int> PII; int m,n;//因为要单独封装一个BFS bool check[301][301];//标记数组 看看哪些点是选过的 int numIslands(vector<vector<char>>& grid) { //ret统计一共有多少个联通块 int ret=0; //直接修改原数组的话 可能会有问题 m=grid.size(); n=grid[0].size(); for(int i=0;i<m;++i) for(int j=0;j<n;++j) if(grid[i][j]=='1'&&check[i][j]==false) { ++ret; bfs(grid,i,j); } return ret; } void bfs(vector<vector<char>>& grid,int i,int j) { queue<PII> q;//队列统计下标实现BFS q.emplace(i,j); check[i][j]=true; while(!q.empty()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]=='1'&&check[x][y]==false) { q.emplace(x,y); check[x][y]=true; } } } } };三、岛屿的最大面积

我们需要统计每个岛屿的大小,所以我们可以将bfs单独封装成一个函数,然后利用他的返回值返回岛屿的大小,在主函数中去更新找到最大值。
class Solution { public: int dx[4]={1,-1,0,0}; int dy[4]={0,0,1,-1}; typedef pair<int,int> PII; int m,n;//因为要单独封装一个BFS bool check[50][50];//标记数组 看看哪些点是选过的 int maxAreaOfIsland(vector<vector<int>>& grid) { int ret=0;//统计最大岛屿数量 m=grid.size(),n=grid[0].size(); for(int i=0;i<m;++i) for(int j=0;j<n;++j) if(grid[i][j]==1&&check[i][j]==false) ret=max(bfs(grid,i,j),ret); return ret; } int bfs(vector<vector<int>>& grid,int i,int j) { queue<PII> q; q.emplace(i,j); check[i][j]=true; int count=1; while(!q.empty()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&check[x][y]==false) { check[x][y]=true; q.emplace(x,y); ++count; } } } return count; } };四、被围绕的区域
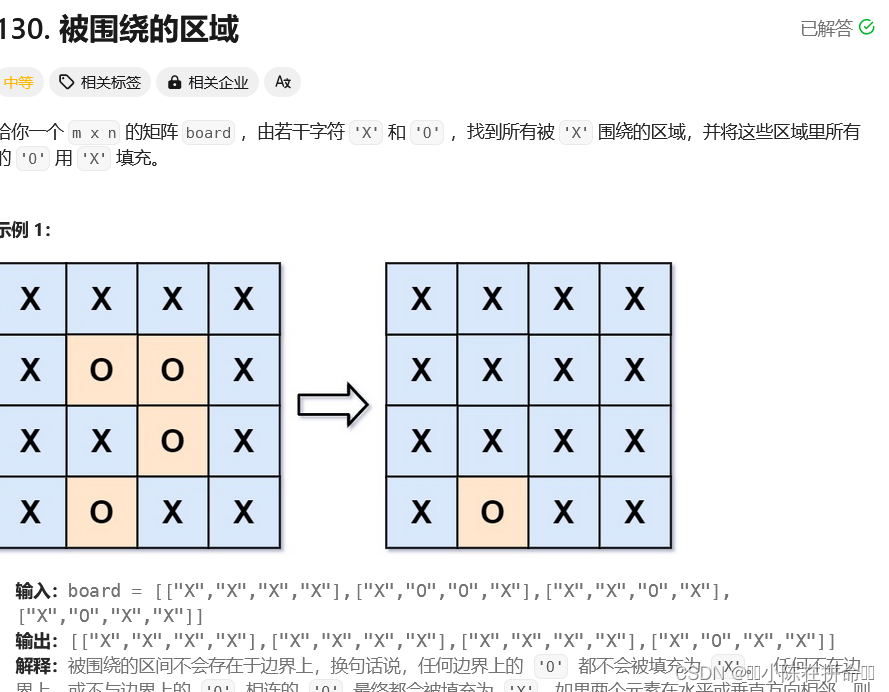
如果直接做的话,我们会发现如果我们处理一个区域的时候一旦触碰到边界,那么就全部需要回头。或者说得先遍历一遍,确认这个联通块没有触碰边界,然后再遍历一次去标记,这样显然效率是很低的。因此我们的解决方案就是正难则反。
(1)先从边界走一波bfs,将O全部修改成 .
(2)然后遍历矩阵(遍历矩阵的时候可以顺便还原,所以这个地方我们就不需要设置标记数组),将剩下的O修改成X,然后将.还原成O。
class Solution { public: const int dx[4]={1,-1,0,0}; const int dy[4]={0,0,1,-1}; typedef pair<int,int> PII; int m,n;//因为要单独封装一个BFS void solve(vector<vector<char>>& board) { m=board.size(),n=board[0].size(); //先处理第一行和最后一行 for(int j=0;j<n;++j) { if(board[0][j]=='O') bfs(board,0,j); if(board[m-1][j]=='O') bfs(board,m-1,j); } //处理第一列和最后一列 for(int i=0;i<m;++i) { if(board[i][0]=='O') bfs(board,i,0); if(board[i][n-1]=='O') bfs(board,i,n-1); } //进行复原 for(int i=0;i<m;++i) for(int j=0;j<n;++j) if(board[i][j]=='O') board[i][j]='X'; else if(board[i][j]=='.') board[i][j]='O'; } void bfs(vector<vector<char>>& board,int i,int j) { queue<PII> q; q.emplace(i,j); board[i][j]='.'; while(!q.empty()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='O') { q.emplace(x,y); board[x][y]='.'; } } } } };五、太平洋大西洋水流问题

如果我们直接做的话,显然需要需要遍历矩阵,然后每遍历一个点就要判断该点是否可以同时流向太平洋和大西洋,显然这样是十分麻烦的。因此我们的思路就是正难则反。
(1)从矩阵的边界开始逆推(从低往高处流)
(2)用两个标记数组进行标记,一个标记表示可以流向太平洋,另一个标记可以流向大西洋,最后我们将两个标记数组都标记过的坐标进行统计并返回即可。
class Solution { public: const int dx[4]={0,0,-1,1}; const int dy[4]={1,-1,0,0}; int m,n; vector<vector<int>> pacificAtlantic(vector<vector<int>>& h) { //正难则反 用两个标记数组,用边界去往中间走,将能走的位置给标记了 //最后两个标记数组都被标记的地方就是我们最终的结果 m=h.size(),n=h[0].size(); //定义两个标记数组 vector<vector<bool>> atl(m,vector<bool>(n)); auto pac=atl; //先探索行 for(int i=0;i<m;++i) { bfs(h,i,0,pac); bfs(h,i,n-1,atl); } //探索列 for(int j=0;j<n;++j) { bfs(h,0,j,pac); bfs(h,m-1,j,atl); } //遍历一下 如果标记数组都存在,就返回结果 vector<vector<int>> ret; for(int i=0;i<m;++i) for(int j=0;j<n;++j) if(pac[i][j]&&atl[i][j]) ret.push_back({i,j}); return ret; } void bfs(vector<vector<int>>& h,int i,int j,vector<vector<bool>>&vis) { queue<pair<int,int>> q; q.emplace(i,j); vis[i][j]=true; while(!q.empty()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&h[x][y]>=h[a][b]&&vis[x][y]==false) { q.emplace(x,y); vis[x][y]=true; } } } } };六、扫雷游戏(重点)

这题用dfs不需要标记数组,而用bfs需要用到标记数组,因为深度优先会将一个方格能扩展的都给扩展了,此时都在数组中会进行修改,但是广度优先是先把要扩展的全都丢进队列,然后再一个个处理,所以bfs需要一个标记数组来帮助我们。
class Solution { public: int dx[8]={0,0,1,-1,1,1,-1,-1}; int dy[8]={1,-1,0,0,1,-1,1,-1}; //周围的八个方向 int m,n; vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) { m=board.size(),n=board[0].size(); int x=click[0],y=click[1]; if(board[x][y]=='M') board[x][y]='X'; else bfs(board,x,y);//不是雷,就向外扩展 return board; } void bfs(vector<vector<char>>& board,int i,int j) { queue<pair<int,int>> q; vector<vector<bool>> vis(m,vector<bool>(n));//标记数组 q.emplace(i,j); vis[i][j]=true; while(!q.empty()) { auto[a,b]=q.front(); q.pop(); int count=0;//数雷 for(int k=0;k<8;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='M') ++count; } if(count) board[a][b]='0'+count; else { //如果是B的话,需要将相邻的都丢到队列中 board[a][b]='B'; for(int k=0;k<8;++k) { int x=dx[k]+a,y=dy[k]+b; if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='E'&&vis[x][y]==false) { q.emplace(x,y); vis[x][y]=true; } } } } } };七、衣柜整理
class Solution { public: const int dx[2]={1,0}; const int dy[2]={0,1}; bool vis[100][100]; int m,n,cnt; int wardrobeFinishing(int _m, int _n, int _cnt) { m=_m,n=_n,cnt=_cnt; int ret=0;//统计需要整理的格子 queue<pair<int,int>> q; q.emplace(0,0); vis[0][0]=true; while(!q.empty()) { auto[a,b]=q.front(); q.pop(); ++ret; for(int k=0;k<2;++k) { int x=dx[k]+a,y=dy[k]+b; if(x<m&&y<n&&vis[x][y]==false&&check(x,y)) { q.emplace(x,y); vis[x][y]=true; } } } return ret; } //检查这个格子能否整理 bool check(int i,int j) { int temp=0; while(i) { temp+=(i%10); i/=10; } while(j) { temp+=(j%10); j/=10; } return temp<=cnt; } };