目录
希尔排序是简单插入排序的一种升级版,它也是用了插入的思想,而插入排序相比冒泡排序和选择排序的效率要高的多,再将它优化为希尔排序后效率跟原来根本就不在一个级别。接下来我们就一起来学习一下希尔排序
一、希尔排序原理
希尔排序的原理是插入排序,接下来先讲一下简单插入排序
简单插入排序原理:
首先假设第一个元素就是一个小数组并且是有序的,然后把第二个元素当做新加入的元素,依次往前遍历把它放在合适的位置保持小数组有序,同理把第三个元素当做新加入的元素,依次往前遍历把它放在合适的位置保持前面的小数组有序,依次重复下去直到把大数组的最后一个元素给放置好,这有点像高等代数里的基底扩充定理,从一个小的空间覆盖到整个大的空间。
动态图:
//简单插入排序 void InsertSort(int* a, int sz) { for (int i = 0; i < sz - 1; i++) { int j = i, tmp = a[i + 1]; while (j >= 0 && tmp < a[j]) { a[j + 1] = a[j--]; } a[j + 1] = tmp; } }如果一个数组储存数据是顺序有序的时候效率是最高的时间复杂度为O(n)。
有的时候该排序遇到一些极端的情况还是比较低效的,比如需要将一组数组进行升序排序,如果这组数据恰好是降序(即逆有序)的话就会很麻烦时间复杂度O(N^2),它需要将新元素前面的所有数据都遍历完。为了解决类似的问题就引入了希尔排序。
二、希尔排序的思路
希尔排序的原理还是插入排序,就是在做简单插入排序之前做一下预处排序,
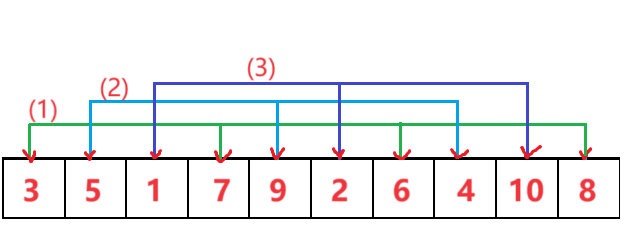
先把数据分组,如上图分为(1),(2),(3)三组,然后分别对这三组进行简单插入排序,这是一次预排序。
那么这三组是如何分出来的呢?主要是涉及到一个增量的问题,如上图的增量是3,在取第(1)组元素时每隔3个元素取一次,第(2)第(3)组同样,直到把每个元素都取到。
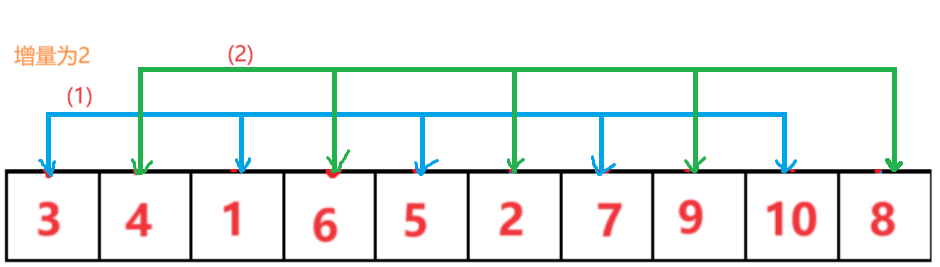
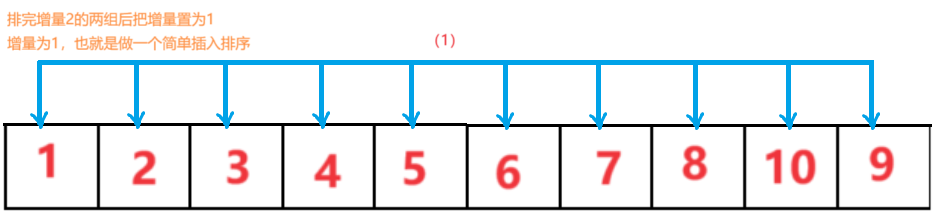
排完上面三组后继续减小增量分组进行简单插入排序,比如排完以3为增量的三组后,再把增量变为2分为二组,最后当增量为1的时候相当于对整个大组做了一个简单插入排序,排完这一趟后这个数组就有序了,希尔排序结束。
三、希尔排序为什么快
简单插入排序的时间复杂度为O(N^2),而希尔排序的时间复杂度大概为O(N^1.3),当然这还与如何取增量有关。
希尔排序确实比之前的简单插入排序所排的组数要多,因为简单插入排序相当于只排了一组,那么它为什么还那么快呢?
因为它大大的减少了数据挪动次数,在做预排序的时候它是以增量的跨度去挪动的,这就使一个数据更快的接近它的准确位置(也就是排序后它该在的位置)。
四、如何取增量
希尔排序的核心就在于通过设定不同的增量序列来优化插入排序的性能。增量序列的选择对排序速度有显著影响。一般来说,增量序列的选择涉及多种策略,而最佳的增量序列并没有一个固定的标准。比较常用效果比较好的增量设定为size/3+1。size为数组长度。
五、源码
#include<stdio.h> //单组排 void ShellSort1(int* a, int sz)//(一组排完再排另一组) { int gap = sz;//增量 while (gap > 1) { gap = gap / 3 + 1; for (int i = 0; i < gap; i++) { for (int j = i; j < sz - gap; j += gap) { int m = j; int tmp = a[j + gap]; while (m >= 0 && tmp < a[m]) { a[m + gap] = a[m]; m -= gap; } a[m + gap] = tmp; } } } } //多组一起排 void ShellSort2(int* a, int sz) { int gap = sz;//增量 while (gap > 1) { gap = gap / 3 + 1; for (int i = 0; i < sz - gap; i++) { int j = i; int tmp = a[i + gap]; while (j >= 0 && tmp < a[j]) { a[j + gap] = a[j]; j -= gap; } a[j + gap] = tmp; } } } int main() { int arr[] = { 8,3,4,9,2,6,5,7,1,10 }; int size = sizeof(arr) / sizeof(int); ShellSort1(arr, size); for (int i = 0; i < size; i++) printf("%d ", arr[i]); return 0; }