文章目录
关系运算
- 关系运算包含
- 关系代数(relational algebra):关系代数是一种过程化查询语言,通过描述对关系的运算来表达查询、获取数据
- 关系演算:非过程化查询语言,通过描述想要获取的数据的信息来获取数据(不需要给出运算过程)
- 关系演算可以分为元组关系演算和域关系演算两种语言
- 为了方便用户查询处理关系数据,定义了结构化查询语言SQL 来操作处理关系数据
关系代数
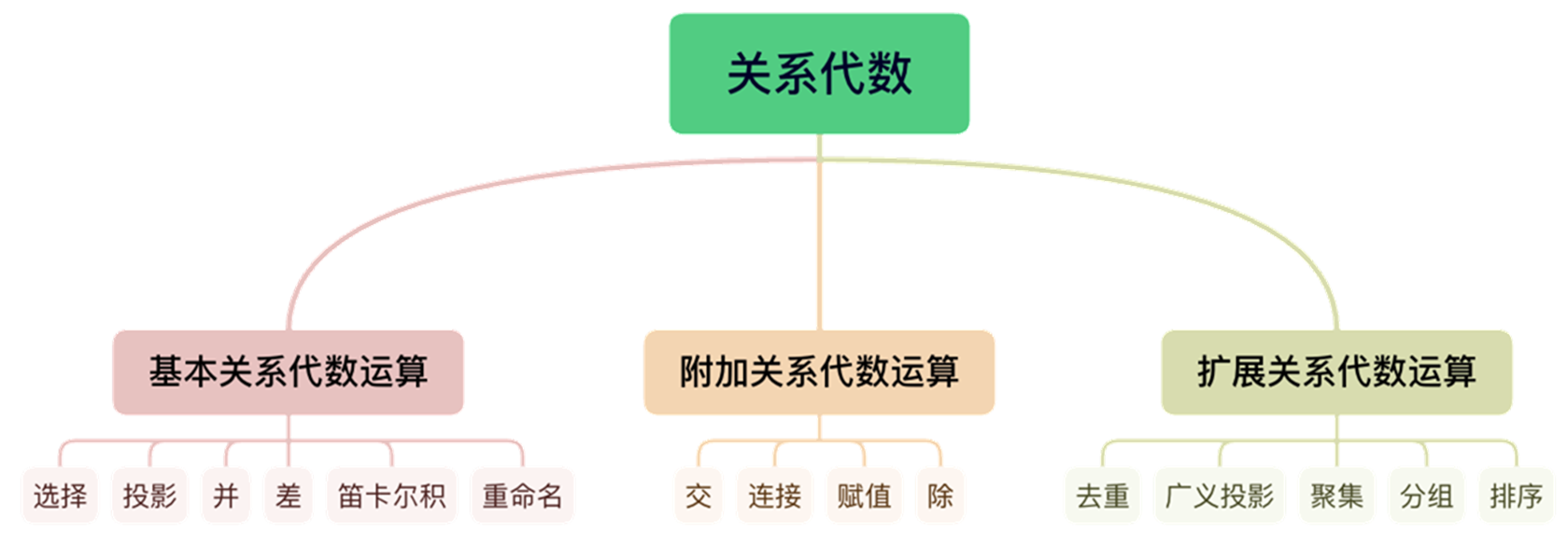
- 关系代数定义了一个关系数据的运算的集合
- 关系运算以一个或者两个关系为输入;输出一个新的关系作为运算结果
- 关系是一个以元组为元素的多重集合(multiset):可能包含重复元素
- 关系代数运算本质上是对多重集合的运算
基本关系代数运算
包括选择、投影、并、差、笛卡尔积和重命名(期中,选择、投影、重命名为一元运算,并、差、笛卡尔积为二元运算)
基本关系代数运算可以用来表达任何传统关系代数运算
选择
选择运算 σ \sigma σ可以从关系 R R R中获取满足条件的元组:
σ p ( R ) = { t ∣ t ∈ R ∧ p ( t ) = True } \sigma_p(R)=\{t\mid t\in R\land p(t)=\text{True}\} σp(R)={t∣t∈R∧p(t)=True}
p p p为选择谓词:
- p p p是由逻辑运算符与 ∧ \land ∧、或 ∨ \lor ∨、非 ¬ \lnot ¬连接的若干原子表达式构成的公式
- 原子表达式的形式为: X □ Y X\ \Box \ Y X □ Y
- X , Y X,Y X,Y:属性名、常量,或者函数值
- □ \Box □为比较运算符,包括 = > < ≠ ≤ ≥ =\ >\ <\ \neq\ \leq\ \geq = > < = ≤ ≥
投影
投影运算 Π \Pi Π可以从关系 R R R中获取某些列组成新的关系:
Π A 1 , A 2 , … , A k ( R ) = { t [ A 1 , A 2 , … , A k ] ∣ t ∈ R } \Pi_{A_1,A_2,\ldots,A_k}(R)=\{t[A_1,A_2,\ldots,A_k]\mid t\in R\} ΠA1,A2,…,Ak(R)={t[A1,A2,…,Ak]∣t∈R}
- A 1 , A 2 , … , A k A_1,A_2,\ldots,A_k A1,A2,…,Ak为R中的属性列
- 返回R中元组在 A 1 , A 2 , … , A k A_1,A_2,\ldots,A_k A1,A2,…,Ak列上的值
- 删除重复元组
并
并运算 ∪ \cup ∪返回两个关系 R R R和 S S S中元组取并集的结果:
R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R\cup S=\{t\mid t\in R\lor t\in S\} R∪S={t∣t∈R∨t∈S}
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同
Union:去重
Union all:不去重
差
差运算 − - −返回在关系R中但是不在关系S中的元组集合:
R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{t\mid t\in R \land t\notin S\} R−S={t∣t∈R∧t∈/S}
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同
笛卡尔积
笛卡尔积运算 × \times ×返回关系R中元组和关系S中的元组做笛卡尔积的结果:
R × S = { ( t , q ) ∣ t ∈ R ∧ q ∈ S } R\times S=\{(t,q)\mid t\in R\ \land\ q\in S\} R×S={(t,q)∣t∈R ∧ q∈S}
- ( t , q ) (t,q) (t,q)为R中元组t和S中元组q拼接在一起得到的元组
- R × S R\times S R×S中有 ∣ R ∣ × ∣ S ∣ |R|\times|S| ∣R∣×∣S∣个元组
例如: instructor × teaches \text{instructor}\times\text{teaches} instructor×teaches
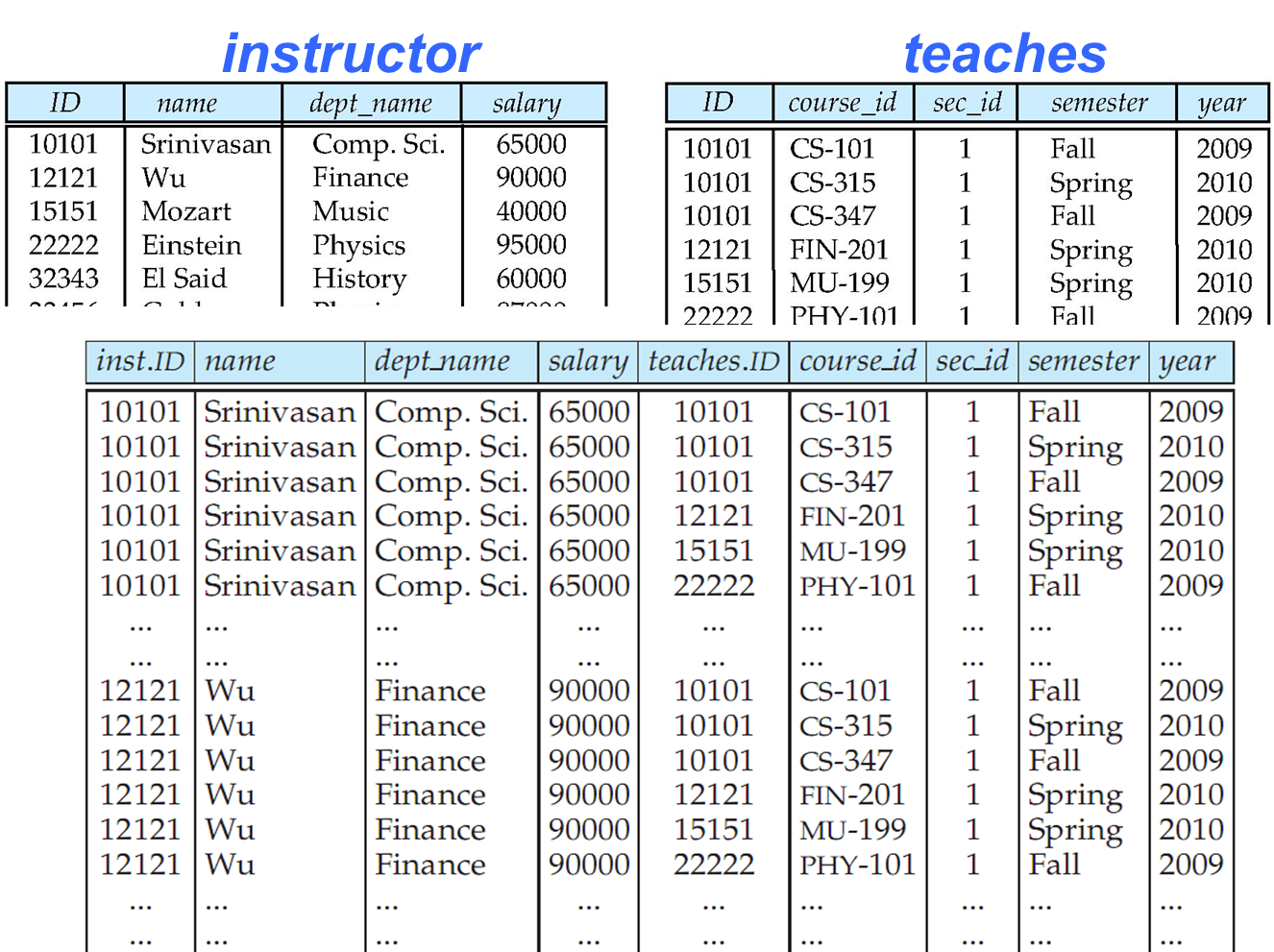
重命名
重命名运算 ρ \rho ρ将关系R重命名为关系S:
ρ S ( A 1 , A 2 , … , A n ) ( R ) \rho_{S(A_1,A_2,\dots,A_n)}(R) ρS(A1,A2,…,An)(R)
- 同时将各属性按照从左到右的顺序重命名为 A 1 , A 2 , … , A n A_1,A_2,\ldots,A_n A1,A2,…,An
- ρ S R \rho_{S}R ρSR:只修改关系名,不修改属性名
附加关系代数运算
- 基本关系代数运算写出来的表达式比较冗长,因此定义了附加关系代数运算
- 附加关系代数运算是由基本关系代数运算导出的运算,可以简化表达式
- 附加关系代数运算和基本关系代数运算的表达能力相同
交
交运算 ∩ \cap ∩返回两个关系R和S中元组取交集的结果:
R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R\cap S=\{t\mid t\in R\land t\in S\} R∩S={t∣t∈R∧t∈S}
- R和S中属性个数要相同
- R和S中的属性应存在一一对应关系
- R中每个属性的域和S中对应属性的域要相同
交运算可以通过差运算来表示: R ∩ S = R − ( R − S ) R\cap S=R-(R-S) R∩S=R−(R−S)
连接
连接运算 ⋈ \Join ⋈返回关系R和S笛卡尔积运算结果中满足一定条件的元组:
R ⋈ p S = { ( t , q ) ∣ t ∈ R ∧ q ∈ S ∧ p ( t , q ) = True } R\Join_{p}S=\{(t,q)\mid t\in R\land q\in S\land p(t,q)=\text{True}\} R⋈pS={(t,q)∣t∈R∧q∈S∧p(t,q)=True}
p p p为选择谓词
- p p p是由逻辑运算符与 ∧ \land ∧、或 ∨ \lor ∨、非 ¬ \lnot ¬连接的若干原子表达式构成的公式
- 原子表达式的形式为: R . X Θ S . Y R.X\ \Theta\ S.Y R.X Θ S.Y
- X是R的属性,Y是S的属性,X和Y所属域具有相同的数据类型
- Θ \Theta Θ:比较运算符,包括=、>、<、≥、≤、≠ (当 Θ \Theta Θ为=时,称为等值连接)
连接运算可通过组合笛卡尔积运算和选择运算来表示
- 自然连接
- 自然连接是一种特殊的等值连接
- 将连接条件指定为R和S中属性名相同的列做等值连接,因此p可省略
- 外连接:连接运算的扩展,可以处理缺失值
- 左外连接(R⟕S)会保留左边关系R的所有元组,对于R中的元组,若在S中没有在同名属性上取值相同的元组,会用空值来填充S中的属性
- 右外连接(R⟖S)会保留右边关系S的所有元组,对于S中在R中不存在同名属性上取值相同的元组,会用空值来填充R中的属性
- 全外连接(R⟗S)的查询结果是左外连接和右外连接查询结果的并集
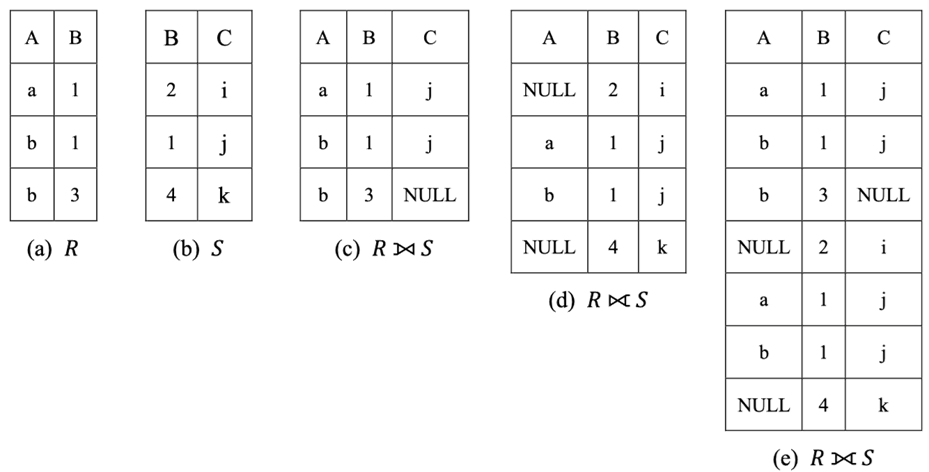
赋值
赋值运算 ← \leftarrow ←将右侧的关系代数表达式结果赋值给左侧的关系变量: T ← E T\leftarrow E T←E
- T为临时关系变量
- E为关系代数表达式
例如:
对学生表和学生选课表进行连接运算,连接的条件为学生表中的Sno列和学生选课表中的Sno列的值相等,并将连接结果赋值给关系变量result
t e m p ← S t u d e n t × S C r e s u l t ← σ S t u d e n t . S n o = S C . S n o ( t e m p ) \begin{aligned} & temp\leftarrow Student\times SC\\ & result\leftarrow \sigma_{Student.Sno=SC.Sno}(temp) \end{aligned} temp←Student×SCresult←σStudent.Sno=SC.Sno(temp)
除
设 R ( A 1 , A 2 , … , A m , B 1 , B 2 , … , B n ) R(A_1,A_2,\dots,A_m,B_1,B_2,\dots,B_n) R(A1,A2,…,Am,B1,B2,…,Bn)和 S ( B 1 , B 2 , … , B n ) S(B_1,B_2,\dots,B_n) S(B1,B2,…,Bn)是两个关系,则 R ÷ S R\div S R÷S的属性为 A 1 , A 2 , … , A m A_1,A_2,…,A_m A1,A2,…,Am,且:
R ÷ S = { t ∣ t ∈ Π A 1 , A 2 , … , A n ( R ) ∧ ( ∀ q ∈ S , ( t , q ) ∈ R ) } R\div S=\{t\mid t\in \Pi_{A_1,A_2,\dots,A_n}(R)\land (\forall q\in S,(t,q)\in R)\} R÷S={t∣t∈ΠA1,A2,…,An(R)∧(∀q∈S,(t,q)∈R)}
- 除运算(÷)会返回R中在属性 A 1 , A 2 , … , A m A_1,A_2,\dots,A_m A1,A2,…,Am上的元组t,其中元组t和关系S中的任意元组q的组合都会出现在关系R中
- 如果S中有R中没有的属性,则无法进行除运算
除运算可以用投影运算和笛卡尔积运算表示:
R ÷ S = Π A 1 , A 2 , … , A n ( R ) − Π A 1 , A 2 , … , A n ( ( Π A 1 , A 2 , … , A n ( R ) × S ) − R ) R\div S=\Pi_{A_1,A_2,\dots,A_n}(R)-\Pi_{A_1,A_2,\dots,A_n}((\Pi_{A_1,A_2,\dots,A_n}(R)\times S)-R) R÷S=ΠA1,A2,…,An(R)−ΠA1,A2,…,An((ΠA1,A2,…,An(R)×S)−R)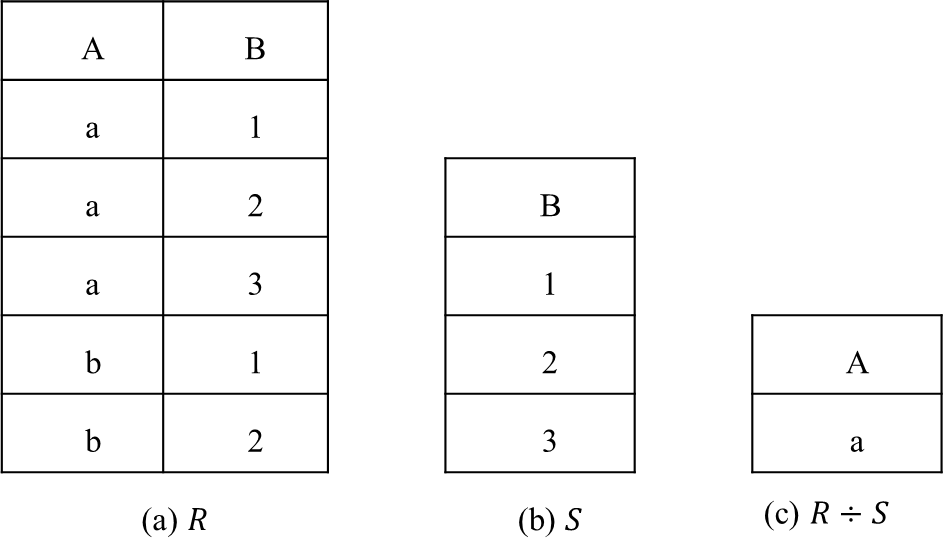
扩展关系代数运算
扩展关系代数运算定义了使用基本关系代数运算和附加关系代数运算无法实现的运算
去重
去重运算 δ \delta δ可以将关系R中的重复元组去除,并返回去除重复元组后的关系: δ ( R ) \delta(R) δ(R)
广义投影
广义投影运算 Π \Pi Π允许在投影列表中使用算术运算和字符串函数等来对投影运算进行扩展:
Π F 1 , F 2 , … , F k ( R ) \Pi_{F_1,F_2,\dots,F_k}(R) ΠF1,F2,…,Fk(R)
- R为关系
- F 1 , F 2 , … , F k F_1,F_2,\dots,F_k F1,F2,…,Fk为包含常量、变量(R中列)、运算符(算术运算符,逻辑运算符,关系运算符)、函数等的多个表达式
聚集
聚集运算 G \mathcal{G} G可以查询关系R按某些列的值聚集在一起的结果:
G F 1 ( A 1 ) , F 2 ( A 2 ) , … , F k ( A k ) ( R ) \mathcal{G}_{F_1(A_1),F_2(A_2),\dots,F_k(A_k)}(R) GF1(A1),F2(A2),…,Fk(Ak)(R)
- A 1 , A 2 , … , A k A_1,A_2,\dots,A_k A1,A2,…,Ak为R中的属性列
- F i F_i Fi为作用在属性 A i A_i Ai上的聚集函数(1≤i≤k)
常见的聚集函数包括count, sum, avg, min, max等
聚集函数对空值NULL的处理:
count()
count(*):不忽略空值count(某个字段):忽略空值sum():可以对单个/多个列求和
- 忽略NULL值,且当对多个列运算求和时,如果运算的列中任意一列的值为NULL,则忽略这行的记录
- 例如:
sum(A+B+C),A、B、C 为三列,如果某行记录中A列值为NULL,则不统计这行avg():忽略NULL值,而不是将其作为0参与计算min(),max():忽略NULL值
分组
分组运算首先对关系R中的元组按照某些列的值进行分组,然后在各组上应用聚集运算:
G 1 , G 2 , … , G l G F 1 ( A 1 ) , F 2 ( A 2 ) , … , F k ( A k ) ( R ) _{G_1,G_2,\dots,G_l}\mathcal{G}_{F_1(A_1),F_2(A_2),\dots,F_k(A_k)}(R) G1,G2,…,GlGF1(A1),F2(A2),…,Fk(Ak)(R)
- G 1 , G 2 , … , G l G_1,G_2,…,G_l G1,G2,…,Gl是用来分组的一系列属性,为R中的列,在这些列上取值都相同的元组将被分到同一组
- A 1 , A 2 , … , A k A_1,A_2,\dots,A_k A1,A2,…,Ak为R中的属性列, F i F_i Fi为作用在属性 A i A_i Ai上的聚集函数(1≤i≤k)
- 查询结果中会包含 G 1 , G 2 , … , G l G_1,G_2,\dots,G_l G1,G2,…,Gl和 F 1 ( A 1 ) , F 2 ( A 2 ) , … , F k ( A k ) F_1 (A_1 ),F_2 (A_2 ),\dots,F_k (A_k ) F1(A1),F2(A2),…,Fk(Ak)列
排序
排序运算 τ \tau τ将关系R中的元组按照一列或多列的值排序: τ A 1 , A 2 , … , A k ( R ) \tau_{A_1,A_2,\dots,A_k}(R) τA1,A2,…,Ak(R)
- A 1 , A 2 , … , A k A_1,A_2,\dots,A_k A1,A2,…,Ak是用来排序的列
- 首先将R中的元组按照 A 1 A_1 A1的值排序,对于 A 1 A_1 A1列取值相同的元组,按照 A 2 A_2 A2的值排序,以此类推。
注意:排序运算 τ \tau τ是按照 A i A_i Ai的升序排列的,也就是从小到大排列。
总结
| 关系代数运算 | 表达式 |
|---|---|
| 选择 | σ p ( R ) = { t ∣ t ∈ R ∧ p ( t ) = True } \sigma_p(R)=\{t\mid t\in R\land p(t)=\text{True}\} σp(R)={t∣t∈R∧p(t)=True} |
| 投影 | Π A 1 , A 2 , … , A k ( R ) = { t [ A 1 , A 2 , … , A k ] ∣ t ∈ R } \Pi_{A_1,A_2,\ldots,A_k}(R)=\{t[A_1,A_2,\ldots,A_k]\mid t\in R\} ΠA1,A2,…,Ak(R)={t[A1,A2,…,Ak]∣t∈R} |
| 并 | R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R\cup S=\{t\mid t\in R\lor t\in S\} R∪S={t∣t∈R∨t∈S} |
| 差 | R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{t\mid t\in R \land t\notin S\} R−S={t∣t∈R∧t∈/S} |
| 笛卡尔积 | R × S = { ( t , q ) ∣ t ∈ R ∧ q ∈ S } R\times S=\{(t,q)\mid t\in R\ \land\ q\in S\} R×S={(t,q)∣t∈R ∧ q∈S} |
| 重命名 | ρ S ( A 1 , A 2 , … , A n ) ( R ) \rho_{S(A_1,A_2,\dots,A_n)}(R) ρS(A1,A2,…,An)(R) |
| 交 | R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R\cap S=\{t\mid t\in R\land t\in S\} R∩S={t∣t∈R∧t∈S} |
| 连接 | R ⋈ p S = { ( t , q ) ∣ t ∈ R ∧ q ∈ S ∧ p ( t , q ) = True } R\Join_{p}S=\{(t,q)\mid t\in R\land q\in S\land p(t,q)=\text{True}\} R⋈pS={(t,q)∣t∈R∧q∈S∧p(t,q)=True} |
| 赋值 | T ← E T\leftarrow E T←E |
| 除 | R ÷ S = { t ∣ t ∈ Π A 1 , A 2 , … , A n ( R ) ∧ ( ∀ q ∈ S , ( t , q ) ∈ R ) } R\div S=\{t\mid t\in \Pi_{A_1,A_2,\dots,A_n}(R)\land (\forall q\in S,(t,q)\in R)\} R÷S={t∣t∈ΠA1,A2,…,An(R)∧(∀q∈S,(t,q)∈R)} |
| 去重 | δ ( R ) \delta(R) δ(R) |
| 广义投影 | Π F 1 , F 2 , … , F k ( R ) \Pi_{F_1,F_2,\dots,F_k}(R) ΠF1,F2,…,Fk(R) |
| 聚集 | G F 1 ( A 1 ) , F 2 ( A 2 ) , … , F k ( A k ) ( R ) \mathcal{G}_{F_1(A_1),F_2(A_2),\dots,F_k(A_k)}(R) GF1(A1),F2(A2),…,Fk(Ak)(R) |
| 分组 | G 1 , G 2 , … , G l G F 1 ( A 1 ) , F 2 ( A 2 ) , … , F k ( A k ) ( R ) _{G_1,G_2,\dots,G_l}\mathcal{G}_{F_1(A_1),F_2(A_2),\dots,F_k(A_k)}(R) G1,G2,…,GlGF1(A1),F2(A2),…,Fk(Ak)(R) |
| 排序 | τ A 1 , A 2 , … , A k ( R ) \tau_{A_1,A_2,\dots,A_k}(R) τA1,A2,…,Ak(R) |
元组关系演算
- 关系代数是一种过程化查询语言,通过在关系代数表达式中指定一个运算的序列,并按照此序列依次执行,可以得到查询的结果
- 元组关系演算是非过程化查询语言,只描述想要获取数据的信息,不描述获取信息的具体过程
元组关系演算表达式的定义为: { t ∣ P ( t ) } \{t\mid P(t)\} {t∣P(t)}
- 上述表达式返回所有使得公式P为真的元组t的集合
- P由原子公式组成,原子公式可以是以下形式之一:
- t ∈ R t\in R t∈R:其中t是元组变量,R是关系
- t [ x ] Θ s [ y ] t[x]\Theta s[y] t[x]Θs[y]:其中t和s是元组变量,x是t所属的关系的属性,y是s所属的关系的属性, Θ \Theta Θ是比较运算符
- t [ x ] Θ c t[x]\Theta c t[x]Θc,其中t,x, Θ \Theta Θ同上,c是属性x的域中的常量

域关系演算
- 域关系演算也是非过程化查询语言
- 域关系演算使用属性域中取值的域变量来代替元组关系演算中的元组变量
域关系演算表达式的定义为: { < x 1 , x 2 , … , x k > ∣ P ( x 1 , x 2 , … , x k ) } \{<x_1,x_2,\dots,x_k>\mid P(x_1,x_2,\dots,x_k)\} {<x1,x2,…,xk>∣P(x1,x2,…,xk)}
- 其中 x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk均为域变量, P P P是由原子公式组成的公式
- 上述表达式返回所有使得公式 P P P为真的域变量 x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk组成的元组的集合
- 原子公式可以是以下形式之一:
- < x 1 , x 2 , … , x k > ∈ R <x_1,x_2,\dots,x_k>\in R <x1,x2,…,xk>∈R,其中R是包含k个属性的关系, x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk为域变量或域常量
- x Θ y x\ \Theta\ y x Θ y,其中x和y是域变量, Θ \Theta Θ是比较运算符(包括>,<,=,≥,≤,≠)
- x Θ c x\ \Theta\ c x Θ c,其中x, Θ \Theta Θ同上,c是x所属属性的属性域中的常量

