阅读量:2
如果从数据的散点图上发现 y 与 x 呈较明显的二次(或高次)函数关系,或者用线性回归的效果不太好,就可以选用多项式回归。
1 一元多项式回归
一元多项式回归可用命令 polyfit 实现。
示例:

首先,画出原始数据散点图:
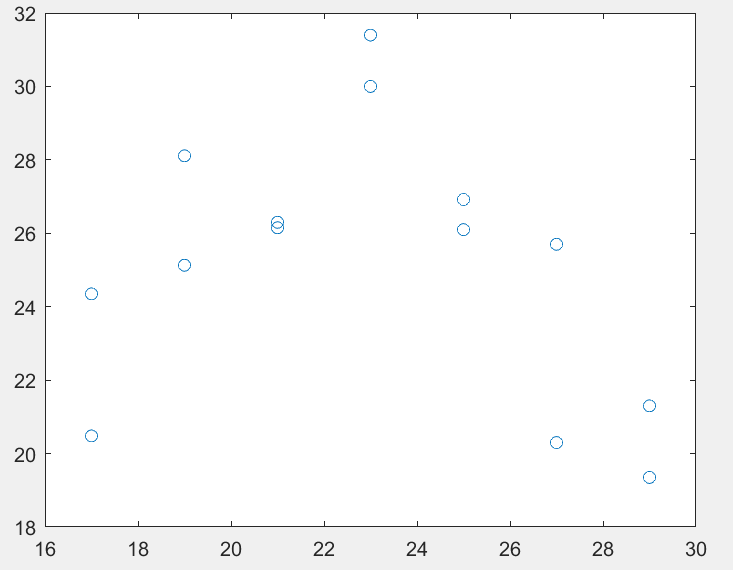
数据的散点图明显地呈现两端低中间高的形状,所以应拟合一条二次曲线。 选用二次模型:
![]()
clc,clear; x0=17:2:29;x0=[x0,x0]; y0=[20.48 25.13 26.15 30.0 26.1 20.3 19.35... 24.35 28.11 26.3 31.4 26.92 25.7 21.3]; [p,s]=polyfit(x0,y0,2); p [y,delta]=polyconf(p,x0,s); y polytool(x0,y0,2)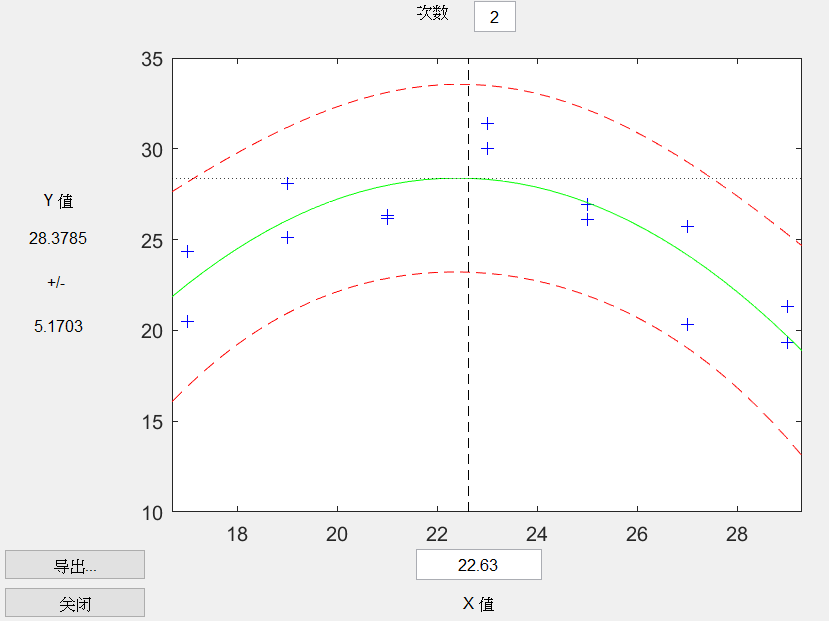
结果显示:

即 a2 = − 0.2003 , a1 =8.9782 ,a0 = −72.2150。
上图得到的是y 的拟合值,及预测值 y 的置信区间半径delta。在画面中绿色曲线为拟合曲线,它两侧的红线是 y 的置信区间。
2 多元二项式回归
统计工具箱提供了一个作多元二项式回归的命令rstool,它也产生一个交互式画面, 并输出有关信息,用法是 :
rstool(x,y,model,alpha)
其中输入数据x,y分别为n × m 矩阵和n 维向量,alpha为显著性水平α (缺省时设定为 0.05),model由下列4个模型中选择1个(用字符串输入,缺省时设定为线性模型)
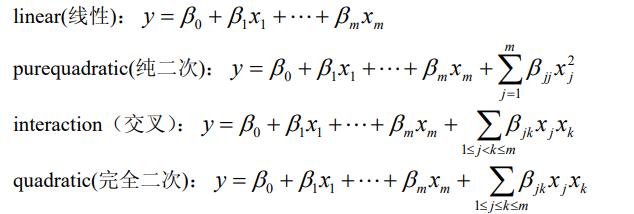
示例,在上一篇中使用了多元线性模型,这次选择纯二次模型来看一下效果:
![]()
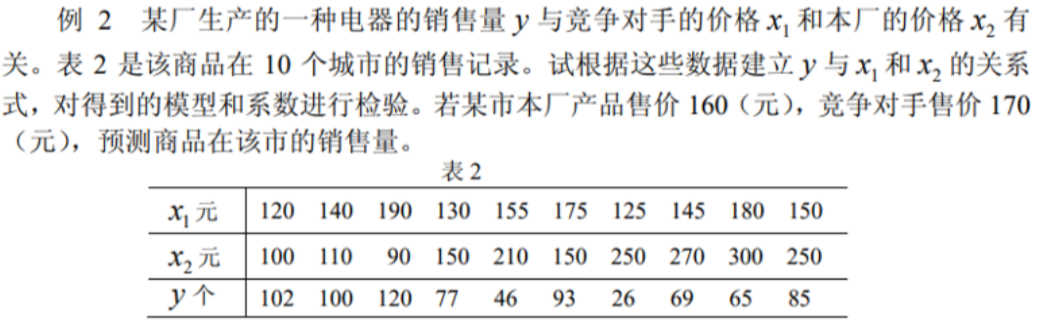
clc,clear; x1=[120 140 190 130 155 175 125 145 180 150]'; x2=[100 110 90 150 210 150 250 270 300 250]'; y=[102 100 120 77 46 93 26 69 65 85]'; x=[x1 x2]; rstool(x,y,'purequadratic') 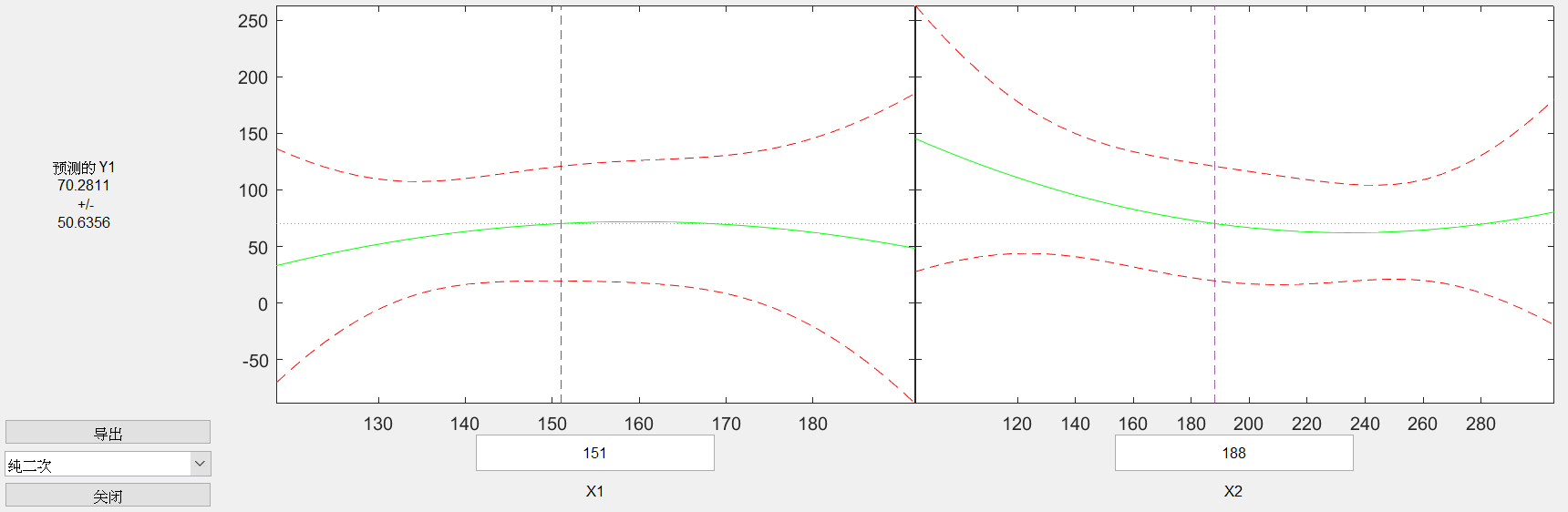 运行结果:
运行结果:
beta =-312.5871 7.2701 -1.7337 -0.0228 0.0037
rmse =16.6436
经对比发现,均方根误差小于上一篇中的多元线性回归拟合的误差,所以纯二次模型效果更好。
