初阶数据结构速成

本篇文章算是对初阶数据结构的总结，内容较多，请耐心观看

基础概念部分

顺序表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是⼀种在实际中⼴泛使 ⽤的数据结构，常⻅的线性表：顺序表、链表、栈、队列、字符串... 顺序表的底层结构是数组，对数组的封装，实现了常⽤的增删改查等接⼝

链表

概念：链表是⼀种物理存储结构上⾮连续、⾮顺序的存储结构，数据元素的逻辑顺序是通过链表 中的指针链接次序实现的 。

栈和队列

栈

概念：进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。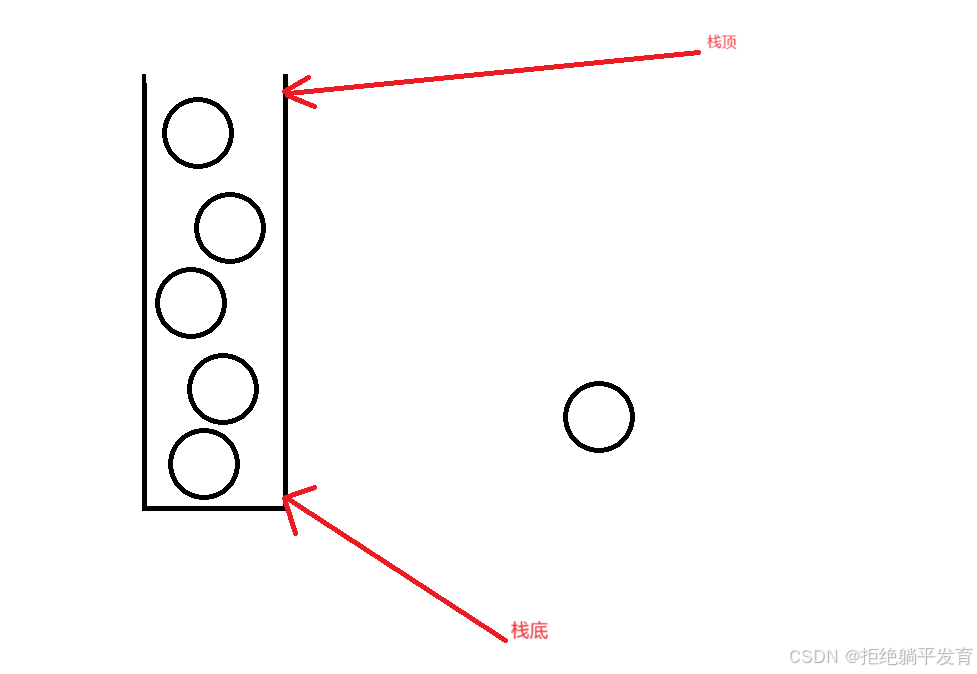

特点

1. 输入和输出都在同一端 2. 先进后出

队列

概念：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头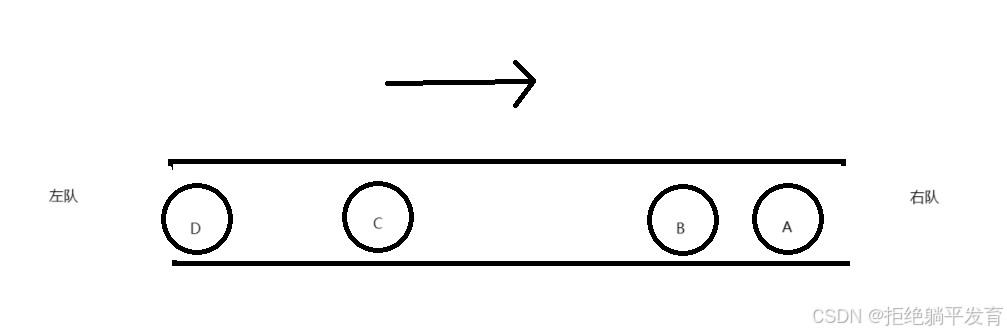

特点

先进先出

树

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合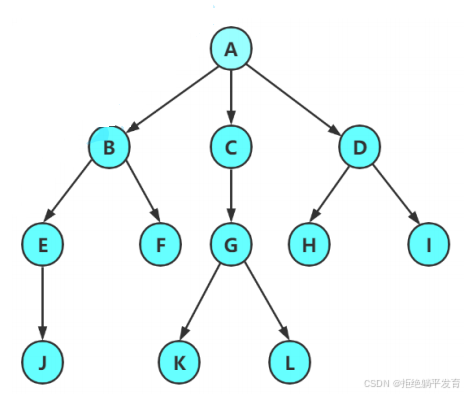

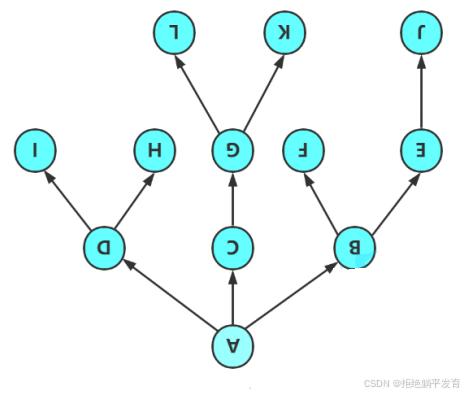
这两个图只是方便大家理解的。

堆 

将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。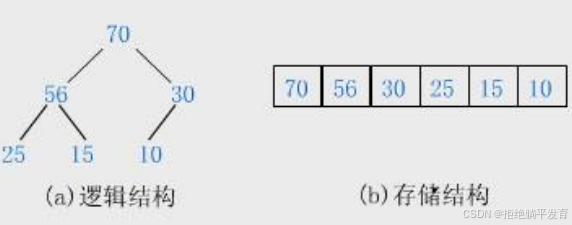

二叉树

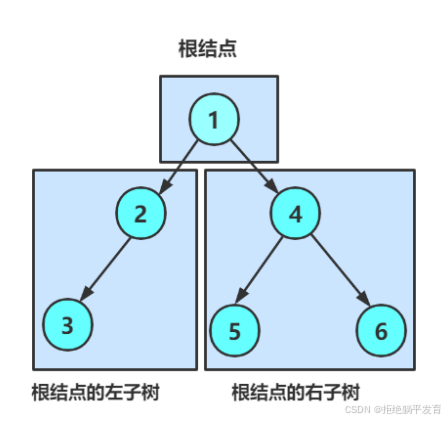
几个重要概念

1. 满二叉树：一个二叉树的层数为K，且结点总数是2的k次 - 1，则它就是满二叉树。

2. 完全二叉树：当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树

3.结点的度： 结点含有的子树的个数

4. 结点的层次： 从根节点开始数

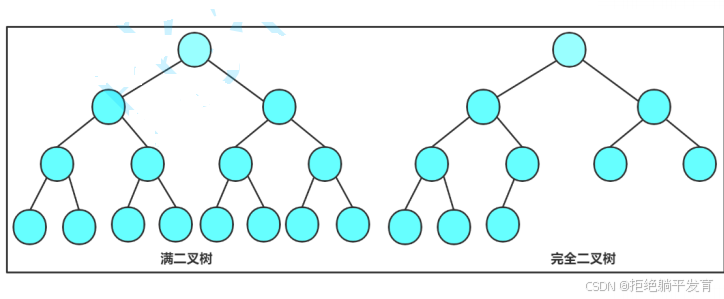
二叉树的特性

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 个结点. 2. 若规定根结点的层数为1，则深度为h的二叉树的最大结点数是 . 3. 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有 ＝ ＋1

实操部分

顾名思义，数据结构是又有数据又有结构体因此初阶数据结构的每一部分内容的结构体给大家放在下方

各种初阶数据结构的结构体部分

顺序表

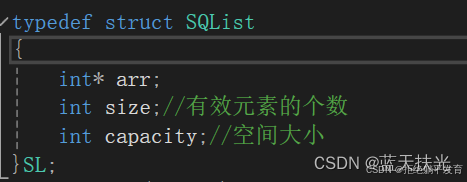
结构体内的元素：数组、有效的元素个数、空间大小

链表

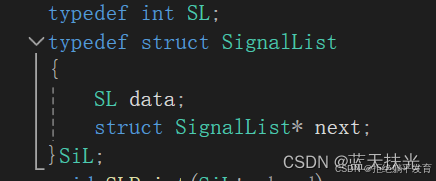
结构体内的元素： 数、指向下一个节点的next指针

栈

队列

初始化以及销毁的思路部分

这里呢我也是找了以前写过的文章，给大家串一串这个部分该怎么写代码

初始化部分

将结构体内的元素进行初始化，eg. 结构体内的数组、指针之类的置为空，剩余的如空间、计数器等整型变量置为0即可，注意初始化前必须声明结构体不为空

销毁部分

先声明结构体以及需要释放的不为空，然后还原回与初始化相同即可。

当然这里的销毁具体情况还需要具体分析，如链表就是需要具体情况具体分析

插入部分

插入的前置条件

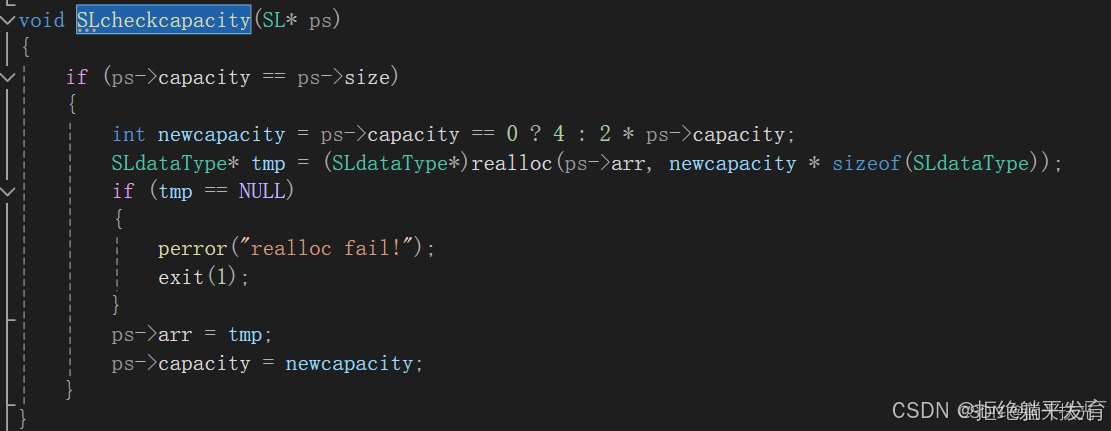
这个部分则是判断空间是否充足，那么这里的逻辑我就不继续讲解了，相信学到这里的小伙伴都是可以靠自己看懂这个代码的，当然啦如果又不懂的小伙伴可以评论区留言

插入数据

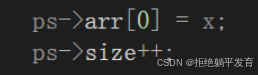
在空间充足的情况下 通过赋值的方式将数据插入，同时别忘了有效数字个数要加一哦。

当然除了上面那种写法外也可以写成：ps->arr[ps->size++] = x;

删除部分

首先需要声明你所要删除的结构体、有效长度、指针等等不为空，通过覆盖、释放函数等手段对其进行删除，有有效长度的需要减一，如果是指针，则需要释放并置空后，在指向下一个节点。

查找部分

这个部分先前是没怎么讲解过，那么我们先来看下实现这个函数，它的新参有哪些

从图中我们可以看出需要的有结构体和需要查找的参数，那么只需要遍历即可（如遍历数组，遍历链表等等）。当找到与我们所要寻找的参数数值相同时，即可返回（该结点等等）即可

以上这些仅仅是思路，如果你是属于那种没有思路，那么这篇文章就很适合你，此外光有这些还不够，最主要的就是画图，需要根据要求进行画图分析，然后将图解转换成代码

那么初阶数据结构系列的文章正式完结