阅读量:4
用红黑树封装map、set
1. 红黑树
- set是K模型,map是KV模型,二者底层都是使用红黑树来实现的,所以我们可以将红黑树设置为模板,即:set、map复用同一个类模板的红黑树。
1.1 模板参数的控制
1.1.1 Value
- Value决定你是k模型的set、还是KV模型的map。

enum Color { //枚举,一一列举出事物具有的所有可能 Red, //枚举常量,给枚举变量进行赋值 Black, }; template<class T>//红黑树的节点 struct RBTreeNode { typedef RBTreeNode<T> Node; //三叉链-》优点:便于查找孩子、父亲节点 Node* _left; //该节点的左孩子 Node* _right; //该节点的右孩子 Node* _parent; //该节点的父亲,便于向上更新 T _data; Color _col; RBTreeNode(const T& data, Color col = Red) //构造函数 :_data(data) , _left(nullptr) , _right(nullptr) , _parent(nullptr) , _col(col) //默认新插入节点的颜色为红色 { } }; //Value决定你是k模型的set、还是KV模型的map template<class K, class T, class KeyOfT> class RBTree { public: typedef RBTreeNode<T> Node; }; template<class K> class set{ //K模型 public: private: //set中的key不允许被修改 RBTree<K, const K, SetKeyOfT> _t; //红黑树对象 }; } template<class K, class V> class map { //KV模型 public: private: //map中的key不允许被修改 RBTree<K, pair<const K, V>, MapKeyOfT> _t; //红黑树对象 }; }; 1.1.2 KeyOfValue
- KeyOfT : 取出Value对象中的key。

// KeyOfT : 取出Value对象中的key template<class K, class T, class KeyOfT> class RBTree { }; struct SetKeyOfT{ const K& operator()(const K& key) { return key; //key } }; struct MapKeyOfT { const K& operator()(const pair<K, V>& kv) { return kv.first; //pair中的key } }; 1.2 正向迭代器
1.2.1 构造函数
💡RBTreeIterator(Node* node) ;
RBTreeIterator(Node* node) //构造函数,单参数构造函数支持隐式类型转化 :_node(node) { } - Tips : 单参数构造函数支持隐式类型转换 Node*->iterator 。
1.2.2 begin()+end()
💡iterator begin( ) ;
- 功能:返回红黑树中最左节点(左孩子必为空)的迭代器。
- Tips:set、map对象为非const对象,就调用begin()、end()。
iterator begin() //红黑树最左节点 { Node* subLeft = _root; while (subLeft && subLeft->_left) subLeft = subLeft->_left; return iterator(subLeft); } 💡iterator end( ) ;
- 功能:返回最后一个元素的下一个的迭代器(空指针)。
iterator end() //空指针 左闭右开[begin,end) { return iterator(nullptr); } 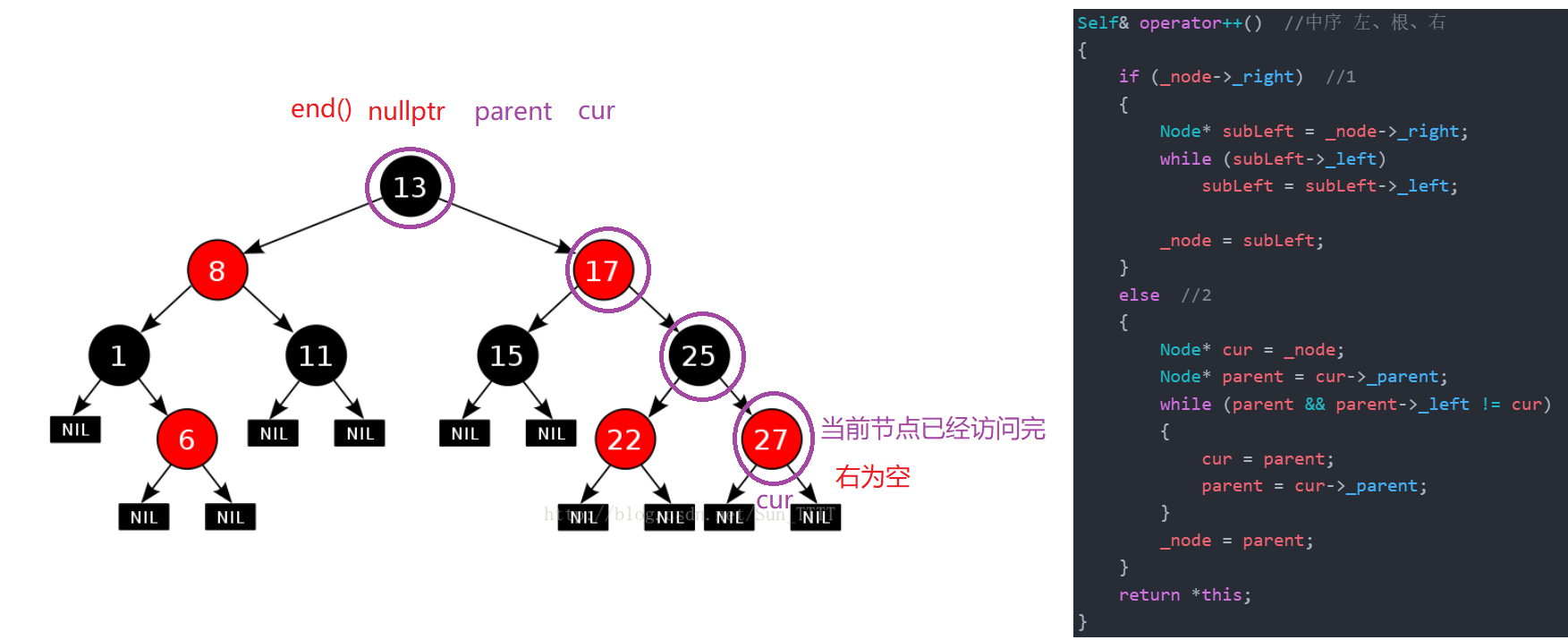
1.2.3 operator++()
/*1.右不为空,下一个为该节点右子树的最左节点 ; * 2.右为空,说明该节点所在的子树已经访问完了,若该节点为父亲的右,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的左,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲左*/ Self& operator++() //中序 左、根、右 { if (_node->_right) //1 { Node* subLeft = _node->_right; while (subLeft->_left) subLeft = subLeft->_left; _node = subLeft; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_left != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } - 中序遍历,左、根、右。
情况一:右不为空,下一个为该节点右子树的最左节点 ;
情况二:右为空,说明该节点所在的子树已经访问完了,若该节点为父亲的右,说明该父亲所在的子树也访问完了,继续往上找,直到该节点为父亲的左,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲左。
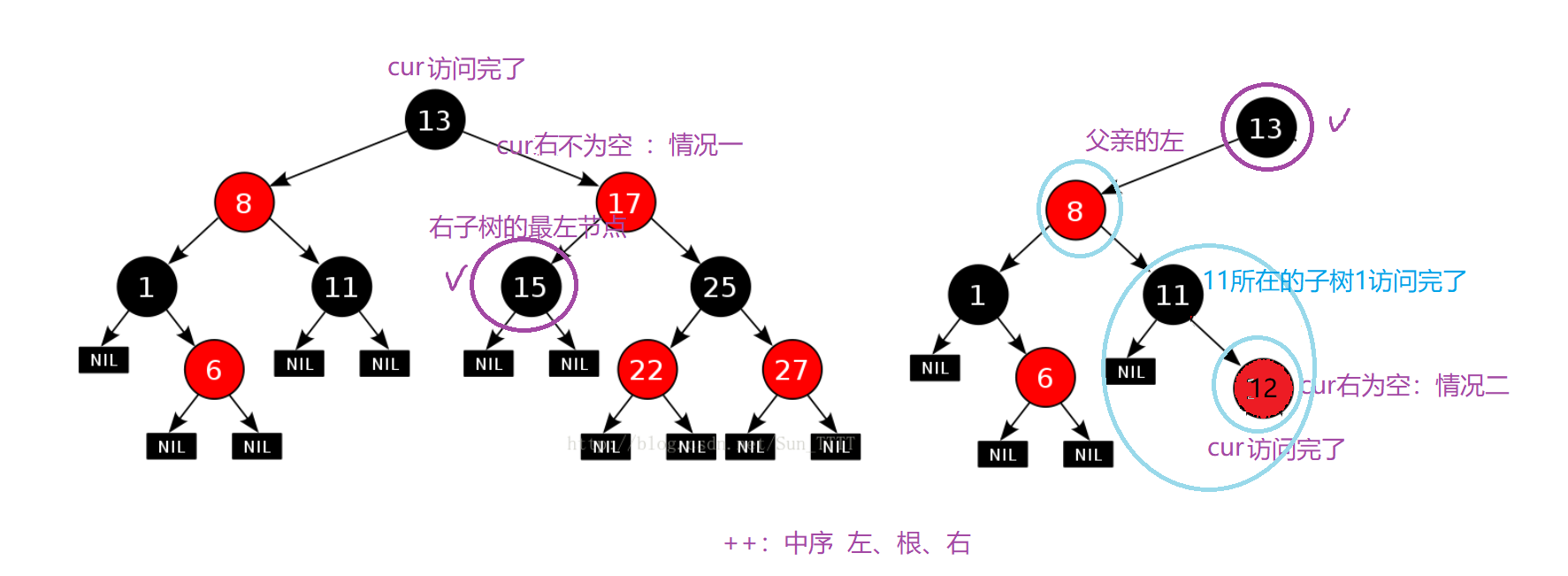
1.2.4 operator–()
/*1.左不为空,下一个为该节点左子树的最右节点 ; * 2.左为空,说明该节点所在的子树已经访问完了,若该节点为父亲的左,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的右,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲右*/ Self& operator--() //中序 左、根、右 --与++逻辑相反 { if (_node->_left) //1 { Node* subRight = _node->_left; while (subRight->_right) subRight = subRight->_right; _node = subRight; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_right != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } 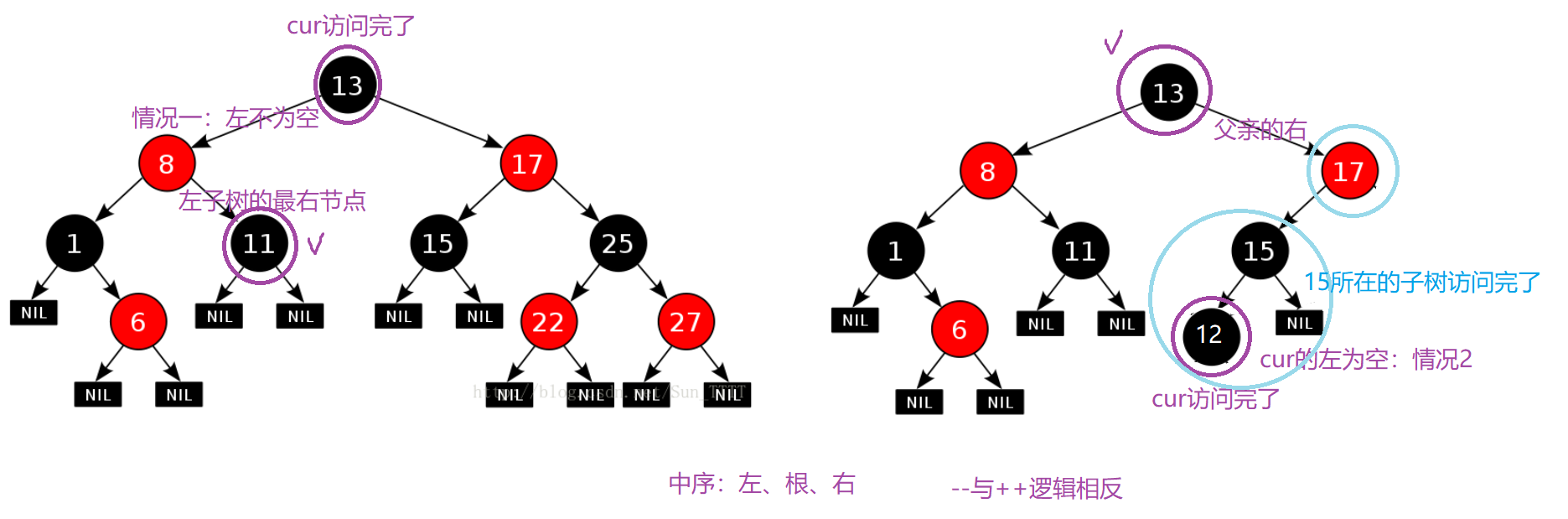
1.2.5 operator*()
Ref operator*() { return _node->_data; } 1.2.6 operator->()
Ptr operator->() //结构体指针,data为结构体 { return &_node->_data; } 1.2.7 operator==()
bool operator==(const Self& rb) { return _node == rb._node; } 1.2.8 operator!=()
bool operator!=(const Self& rb) { return _node != rb._node; } 1.2.9 总代码
template<class T, class Ref, class Ptr> struct RBTreeIterator //红黑树的正向迭代器 { typedef RBTreeNode<T> Node; typedef RBTreeIterator<T, Ref, Ptr> Self; Node* _node; RBTreeIterator(Node* node) //构造函数,单参数构造函数支持隐式类型转化 :_node(node) { } Ref operator*() { return _node->_data; } Ptr operator->() //结构体指针,data为结构体 { return &_node->_data; } /*1.右不为空,下一个为该节点右子树的最左节点 ; * 2.右为空,说明该节点所在的子树已经访问完了,若该节点为父亲的右,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的左,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲左*/ Self& operator++() //中序 左、根、右 { if (_node->_right) //1 { Node* subLeft = _node->_right; while (subLeft->_left) subLeft = subLeft->_left; _node = subLeft; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_left != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } /*1.左不为空,下一个为该节点左子树的最右节点 ; * 2.左为空,说明该节点所在的子树已经访问完了,若该节点为父亲的左,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的右,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲右*/ Self& operator--() //中序 左、根、右 --与++逻辑相反 { if (_node->_left) //1 { Node* subRight = _node->_left; while (subRight->_right) subRight = subRight->_right; _node = subRight; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_right != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } bool operator!=(const Self& rb) { return _node != rb._node; } bool operator==(const Self& rb) { return _node == rb._node; } }; 1.3 反向迭代器
1.3.1 rbegin()+rend()
💡reverse_iterator rbegin( ) ;
- 功能:返回红黑树中最右节点(右孩子必为空)的迭代器。
reverse_iterator rbegin() //红黑树最右节点,因为此处反向迭代器*,是直接调用正向迭代器* [rbegin,erend) { Node* subRight = _root; while (subRight && subRight->_right) subRight = subRight->_right; return reverse_iterator(subRight); } 💡reverse_iterator rend( ) ;
- 功能:返回第一个元素的前一个的迭代器(空指针)。
reverse_iterator rend() { return reverse_iterator(nullptr); } 1.3.2 总代码
template<class iterator, class Ref, class Ptr> struct ReverseIterator //红黑树的反向迭代器——适配器 begin = rend、end = rbegin { typedef ReverseIterator<iterator, Ref, Ptr> Self; iterator _it; //适配器 ReverseIterator(iterator it) :_it(it) { } Ref operator*() { return *_it; } Ptr operator->() { return &(operator*()); // } Self& operator++() { --_it; return *this; } Self& operator--() { ++_it; return *this; } bool operator==(const Self& rb) { return _it == rb._it; } bool operator!=(const Self& rb) { return _it != rb._it; } }; 1.4 find()
💡iterator find(const K& key) ;
- 功能:查找。
- 若key在红黑树中,则返回树中与key值相等元素的迭代器,否则,就返回end( )。
iterator find(const K& key) //查找 模板参数K的作用 { KeyOfT kot; Node* cur = _root; while (cur) //先按照二叉搜索树的方式插入 { if (kot(cur->_data) < key) //通仿函数对象调用operator()来获取T中的key cur = cur->_right; else if (kot(cur->_data) > key) cur = cur->_left; else return iterator(cur); //找到了 } return end(); //找不到 } 1.5 insert()
💡pair<iterator,bool> insert(const T& data) ;
- 功能:向红黑树中插入data。

- insert返回值为pair<iterator, bool>,若key(set的key、map的pair的first)在树中存在,因为搜索树中不能出现重复的键值key,所以pair::first指向在树中与key值相等的迭代器,pair::second为false。若key在树中不存在,pair::first指向在树中新插入元素的迭代器,pair::second为true。insert相当于查找。
pair<iterator, bool> insert(const T& data) //插入 { //不能使用引用放回,因为返回值作用域为栈区,传值返回 KeyOfT kot; //仿函数类创建的对象,对象去调用operator() Node* parent = nullptr; Node* cur = _root; while (cur) //先按照二叉搜索树的方式插入 { if (kot(cur->_data) < kot(data)) //通仿函数对象调用operator()来获取T中的key值 { parent = cur; cur = cur->_right; } else if (kot(cur->_data) > kot(data)) { parent = cur; cur = cur->_left; } else { return make_pair(iterator(cur), false); //插入节点已存在,插入失败,返回在树中与该节点值相同的迭代器 } } cur = new Node(data); //注意 insert Node* newnode = cur; //非空树,插入成功,因为要做旋转处理,会导致cur值发生改变,需提前将新节点的位置存储起来 if (parent == nullptr) //空树 { _root = cur; _root->_col = Black; //跟节点为黑 return make_pair(iterator(_root), true); //空树,插入成功,返回新插入节点在树中的迭代器 } if (kot(parent->_data) < kot(cur->_data)) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //记录当前节点的父亲 //更新颜色 //插入结束:1.插入节点的父亲是黑色,因为插入前该树就为红黑树 2.情况一处理完后,cur为根节点,且为黑色 while (parent && parent->_col == Red) { //爷爷一定存在,因为c为红,p为红,所以p一定不是根节点,且一定有父节点 Node* grandfather = parent->_parent; if (parent == grandfather->_left) //旋转需要确定方向 { Node* uncle = grandfather->_right; if (uncle && uncle->_col == Red) //情况一:叔叔存在且为红->无方向(p、u为g的任意边,c为p的任一边) { //cur可能为新增节点,也可能一开始为黑色,cur的子树(下一层为红,下一层为新插入节点)在调整过程中将cur由黑变为红 parent->_col = uncle->_col = Black; //p、u变为黑,g变为红 grandfather->_col = Red; //g可能为根节点(更新结束),也可能为子树(继续向上更新) cur = grandfather; parent = cur->_parent; } else //情况二:叔叔不存在 或者 叔叔存在且为黑 { //叔叔不存在,cur为新增节点 或 cur原来为黑,经子树调整由黑变红 if (parent->_left == cur) //左左——右单旋 { RotateR(grandfather); parent->_col = Black; //p变为黑,g变为红 grandfather->_col = Red; } else //左右——左右单旋 { RotateL(parent); RotateR(grandfather); cur->_col = Black; //c变黑,g变红 grandfather->_col = Red; } break; //更新结束:3.旋转+颜色处理后就是红黑树了 } } else { Node* uncle = grandfather->_left; if (uncle && uncle->_col == Red) { parent->_col = uncle->_col = Black; grandfather->_col = Red; cur = grandfather; parent = cur->_parent; } else { if (parent->_right == cur) //右右——左单旋 { RotateL(grandfather); parent->_col = Black; grandfather->_col = Red; } else //右左——右左单旋 { RotateR(parent); RotateL(grandfather); cur->_col = Black; grandfather->_col = Red; } break; } } } _root->_col = Black; //g为根,颜色变为黑,更新结束 return make_pair(iterator(newnode), true); //情况一,插入节点的父亲为黑,插入结束 } 2. Map
2.1 operator[]
💡V& operator[ ](const K& key) ;
- 功能:访问与key相对应的value值。即可读又可写。
- 原理:operator[ ]底层是通过调用insert( )将键值队插入到map中。如果key存在,插入失败,insert返回与map中key值相同元素的迭代器。如果key不存在,插入成功,insert返回在map中新插入元素的迭代器。operator[ ]最后返回与key值相对应的value值的引用。
- operator[ ] 具有插入、查找、插入+修改、查找+修改功能。
V& operator[](const K& key) //功能:查找+修改、插入+修改 { pair<iterator, bool> ret = _t.insert(make_pair(key, V())); return ret.first->second; } 3. typename作用
- 使用域作用限定符(: : )的两种情况:静态变量、类中typedef的类型。
- 使用typename表示: :后面为类型,不是静态成员
//使用::两种情况:静态变量、类中typedef的类型 typename表示::前面为类型,不是静态成员 typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator; 4. 完整代码
4.1 Map.h
#pragma once #define _CRT_SECURE_NO_WARNINGS 1 #include"RBTree.h" #include<string> namespace zzx { template<class K, class V> class map { //KV模型 public: struct MapKeyOfT { const K& operator()(const pair<K, V>& kv) { return kv.first; //pair中的key } }; //使用::两种情况:静态变量、类中typedef的类型 typename表示::前面为类型,不是静态成员 typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator; //正向迭代器 typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器 iterator begin() { return _t.begin(); } iterator end() { return _t.end(); } reverse_iterator rbegin() { return _t.rbegin(); } reverse_iterator rend() { return _t.rend(); } iterator find(const K& key) //查找 { return _t.find(key); } pair<iterator, bool> insert(pair<const K, V>& kv) //插入 { return _t.insert(kv); } V& operator[](const K& key) //功能:查找+修改、插入+修改 { pair<iterator, bool> ret = _t.insert(make_pair(key, V())); return ret.first->second; } private: //map中的key不允许被修改 RBTree<K, pair<const K, V>, MapKeyOfT> _t; //红黑树对象 }; }; 4.2 Set.h
#pragma once #define _CRT_SECURE_NO_WARNINGS 1 #include"RBTree.h" namespace zzx{ template<class K> class set{ //K模型 public: //仿函数类:比较对象大小,获取对象中的元素—自己手动传递比较逻辑 struct SetKeyOfT{ const K& operator()(const K& key) { return key; //key } }; //使用::两种情况:静态变量、类中typedef的类型 typename表示::后面为类型,不是静态成员 typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator; //正向迭代器 typedef typename RBTree<K, const K, SetKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器 iterator begin() { return _t.begin(); } iterator end() { return _t.end(); } reverse_iterator rbegin() { return _t.rbegin(); } reverse_iterator rend() { return _t.rend(); } iterator find(const K& key) //查找 { return _t.find(key); } pair<iterator, bool> insert(const K& key) //插入 { return _t.insert(key); } private: //set中的key不允许被修改 RBTree<K, const K, SetKeyOfT> _t; //红黑树对象 }; } 4.3 RBTree.h
#pragma once #define _CRT_SECURE_NO_WARNINGS 1 #include<iostream> using namespace std; enum Color { //枚举,一一列举出事物具有的所有可能 Red, //枚举常量,给枚举变量进行赋值 Black, }; template<class T>//红黑树的节点 struct RBTreeNode { typedef RBTreeNode<T> Node; //三叉链-》优点:便于查找孩子、父亲节点 Node* _left; //该节点的左孩子 Node* _right; //该节点的右孩子 Node* _parent; //该节点的父亲,便于向上更新 T _data; Color _col; RBTreeNode(const T& data, Color col = Red) //构造函数 :_data(data) , _left(nullptr) , _right(nullptr) , _parent(nullptr) , _col(col) //默认新插入节点的颜色为红色 { } }; template<class T, class Ref, class Ptr> struct RBTreeIterator //红黑树的正向迭代器 { typedef RBTreeNode<T> Node; typedef RBTreeIterator<T, Ref, Ptr> Self; Node* _node; RBTreeIterator(Node* node) //构造函数,单参数构造函数支持隐式类型转化 :_node(node) { } Ref operator*() { return _node->_data; } Ptr operator->() //结构体指针,data为结构体 { return &_node->_data; } /*1.右不为空,下一个为该节点右子树的最左节点 ; * 2.右为空,说明该节点所在的子树已经访问完了,若该节点为父亲的右,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的左,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲左*/ Self& operator++() //中序 左、根、右 { if (_node->_right) //1 { Node* subLeft = _node->_right; while (subLeft->_left) subLeft = subLeft->_left; _node = subLeft; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_left != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } /*1.左不为空,下一个为该节点左子树的最右节点 ; * 2.左为空,说明该节点所在的子树已经访问完了,若该节点为父亲的左,说明该父亲所在的子树也访问完了,继续往上找, * 直到该节点为父亲的右,则要访问的下一个节点是它的父亲,即:找祖先里面的孩纸 = 父亲右*/ Self& operator--() //中序 左、根、右 --与++逻辑相反 { if (_node->_left) //1 { Node* subRight = _node->_left; while (subRight->_right) subRight = subRight->_right; _node = subRight; } else //2 { Node* cur = _node; Node* parent = cur->_parent; while (parent && parent->_right != cur) { cur = parent; parent = cur->_parent; } _node = parent; } return *this; } bool operator!=(const Self& rb) { return _node != rb._node; } bool operator==(const Self& rb) { return _node == rb._node; } }; template<class iterator, class Ref, class Ptr> struct ReverseIterator //红黑树的反向迭代器——适配器 begin = rend、end = rbegin { typedef ReverseIterator<iterator, Ref, Ptr> Self; iterator _it; //适配器 ReverseIterator(iterator it) :_it(it) { } Ref operator*() { return *_it; } Ptr operator->() { return &(operator*()); // } Self& operator++() { --_it; return *this; } Self& operator--() { ++_it; return *this; } bool operator==(const Self& rb) { return _it == rb._it; } bool operator!=(const Self& rb) { return _it != rb._it; } }; //红黑树的模板参数:T决定你是k模型的set、还是KV模型的map ; KeyOfT:取出T对象中的key ; pair比较:先比较first,在比较second template<class K, class T, class KeyOfT> class RBTree { public: typedef RBTreeNode<T> Node; //正向迭代器 typedef RBTreeIterator<T, T&, T*> iterator; //普通迭代器 typedef RBTreeIterator<T,const T&, const T*> const_iterator; //const迭代器 //反向迭代器 typedef ReverseIterator<iterator, T&, T*> reverse_iterator; typedef ReverseIterator<const_iterator, const T&, const T*> const_reverse_iterator; iterator begin() //红黑树最左节点 { Node* subLeft = _root; while (subLeft && subLeft->_left) subLeft = subLeft->_left; return iterator(subLeft); } iterator end() //空指针 左闭右开[begin,end) { return iterator(nullptr); } const_iterator begin()const { Node* subLeft = _root; while (subLeft && subLeft->_left) subLeft = subLeft->_left; return const_iterator(subLeft); } const_iterator end()const { return const_iterator(nullptr); } reverse_iterator rbegin() //红黑树最右节点,因为此处反向迭代器*,是直接调用正向迭代器* [rbegin,erend) { Node* subRight = _root; while (subRight && subRight->_right) subRight = subRight->_right; return reverse_iterator(subRight); } reverse_iterator rend() { return reverse_iterator(nullptr); } const_reverse_iterator rbegin()const { Node* subRight = _root; while (subRight && subRight->_right) subRight = subRight->_right; return const_reverse_iterator(subRight); } const_reverse_iterator rend()const { return const_reverse_iterator(nullptr); } iterator find(const K& key) //查找 模板参数K的作用 { KeyOfT kot; Node* cur = _root; while (cur) //先按照二叉搜索树的方式插入 { if (kot(cur->_data) < key) //通仿函数对象调用operator()来获取T中的key cur = cur->_right; else if (kot(cur->_data) > key) cur = cur->_left; else return iterator(cur); //找到了 } return end(); //找不到 } void RotateL(Node* parent) //右右—左单旋 { Node* subR = parent->_right; Node* subRL = subR->_left; Node* pphead = parent->_parent; parent->_right = subRL; if (subRL) subRL->_parent = parent; subR->_left = parent; parent->_parent = subR; if (parent == _root) { _root = subR; subR->_parent = nullptr; } else { if (pphead->_left == parent) pphead->_left = subR; else pphead->_right = subR; subR->_parent = pphead; } } void RotateR(Node* parent) //左左—右单旋 { Node* subL = parent->_left; Node* subLR = subL->_right; Node* pphead = parent->_parent; parent->_left = subLR; if (subLR) subLR->_parent = parent; subL->_right = parent; parent->_parent = subL; if (parent == _root) { _root = subL; subL->_parent = nullptr; } else { if (pphead->_left == parent) pphead->_left = subL; else pphead->_right = subL; subL->_parent = pphead; } } void RotateRL(Node* parent) //右左—先右旋再左旋 { Node* subR = parent->_right; Node* subRL = subR->_left; RotateR(subR); RotateL(parent); } void RotateLR(Node* parent) //左右—先左旋再右旋 { Node* subL = parent->_left; Node* subLR = subL->_right; RotateL(subL); RotateR(parent); } pair<iterator, bool> insert(const T& data) //插入 { //不能使用引用放回,因为返回值作用域为栈区,传值返回 KeyOfT kot; //仿函数类创建的对象,对象去调用operator() Node* parent = nullptr; Node* cur = _root; while (cur) //先按照二叉搜索树的方式插入 { if (kot(cur->_data) < kot(data)) //通仿函数对象调用operator()来获取T中的key值 { parent = cur; cur = cur->_right; } else if (kot(cur->_data) > kot(data)) { parent = cur; cur = cur->_left; } else { return make_pair(iterator(cur), false); //插入节点已存在,插入失败,返回在树中与该节点值相同的迭代器 } } cur = new Node(data); //注意 insert Node* newnode = cur; //非空树,插入成功,因为要做旋转处理,会导致cur值发生改变,需提前将新节点的位置存储起来 if (parent == nullptr) //空树 { _root = cur; _root->_col = Black; //跟节点为黑 return make_pair(iterator(_root), true); //空树,插入成功,返回新插入节点在树中的迭代器 } if (kot(parent->_data) < kot(cur->_data)) { parent->_right = cur; } else { parent->_left = cur; } cur->_parent = parent; //记录当前节点的父亲 //更新颜色 //插入结束:1.插入节点的父亲是黑色,因为插入前该树就为红黑树 2.情况一处理完后,cur为根节点,且为黑色 while (parent && parent->_col == Red) { //爷爷一定存在,因为c为红,p为红,所以p一定不是根节点,且一定有父节点 Node* grandfather = parent->_parent; if (parent == grandfather->_left) //旋转需要确定方向 { Node* uncle = grandfather->_right; if (uncle && uncle->_col == Red) //情况一:叔叔存在且为红->无方向(p、u为g的任意边,c为p的任一边) { //cur可能为新增节点,也可能一开始为黑色,cur的子树(下一层为红,下一层为新插入节点)在调整过程中将cur由黑变为红 parent->_col = uncle->_col = Black; //p、u变为黑,g变为红 grandfather->_col = Red; //g可能为根节点(更新结束),也可能为子树(继续向上更新) cur = grandfather; parent = cur->_parent; } else //情况二:叔叔不存在 或者 叔叔存在且为黑 { //叔叔不存在,cur为新增节点 或 cur原来为黑,经子树调整由黑变红 if (parent->_left == cur) //左左——右单旋 { RotateR(grandfather); parent->_col = Black; //p变为黑,g变为红 grandfather->_col = Red; } else //左右——左右单旋 { RotateL(parent); RotateR(grandfather); cur->_col = Black; //c变黑,g变红 grandfather->_col = Red; } break; //更新结束:3.旋转+颜色处理后就是红黑树了 } } else { Node* uncle = grandfather->_left; if (uncle && uncle->_col == Red) { parent->_col = uncle->_col = Black; grandfather->_col = Red; cur = grandfather; parent = cur->_parent; } else { if (parent->_right == cur) //右右——左单旋 { RotateL(grandfather); parent->_col = Black; grandfather->_col = Red; } else //右左——右左单旋 { RotateR(parent); RotateL(grandfather); cur->_col = Black; grandfather->_col = Red; } break; } } } _root->_col = Black; //g为根,颜色变为黑,更新结束 return make_pair(iterator(newnode), true); //情况一,插入节点的父亲为黑,插入结束 } private: Node* _root = nullptr; }; 