第一章 深度学习和神经网络

文章目录

• 第一章 深度学习和神经网络
• • 深度学习
  • • 机器学习和深度学习的区别
    • • 特征提取的角度
      • 数据量的角度
    • 深度学习的应用场景
    • 框架
  • 神经网络
  • • 人工神经网络
    • 神经元
    • • 单层的神经网络
      • 两层的神经网络
      • • 感知机
      • 多层神经网络
      • 那怎么构建人工神经网络中的神经元呢？
      • 激活函数
      • • 总结

第一章 深度学习和神经网络

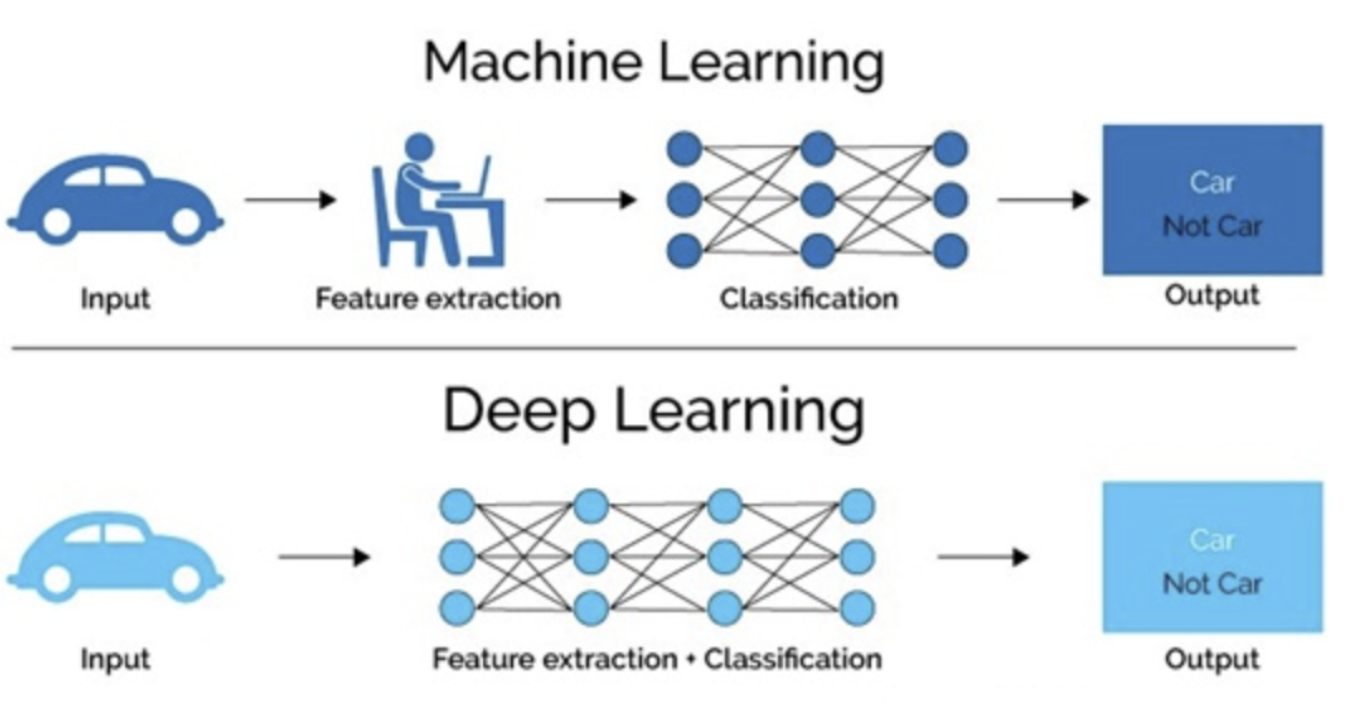
深度学习

深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向，它被引入机器学习器使其更接近于人工智能。

深度学习是机器学习的分支，是一种以人工神经网络为架构，对数据进行特征学习的算法。深度学习它能够自动的帮助我们进行特征抽取。

机器学习和深度学习的区别

特征提取的角度

• 机器学习：人工的特征抽取的过程
• 深度学习：能够自动的进行特征抽取

每个圆圈（蓝色的）他是神经网络里面最小的一个结构，我们把它称之为神经元

假如说我们找了一千个盲人摸象，一千个人每个人摸到的位置都不一样，有的人摸到腿有的人摸到耳朵、鼻子、尾巴…你可以理解为每个人拿到了自己的这样一个特征、自己的这一块面积，这一块面积它们进行随意的组合是不是就可以组合成各种各样的东西，当然不一定组合成大象，除了大象还可能组合成一只猪、牛…很多种可能，那么这个时候刚刚所说的这个过程（随意组合的过程）其实就是我们深度学习做的事情，最开始我们传入的是非常基础的一些特征（每个盲人能摸到自己的这一块），我们把这些特征进行随机组合之后，有可能在输出的这个地方能够得到一只大象，也有可能得不到大象。

那么我们接下来要做的事情就是把这个逻辑构建好之后，就需要传入数据进行训练了，传入数据进行训练过程是在干什么？就是强行的告诉我们这个模型我的输入是这样子的（就是每个盲人摸到的东西），但我们输出是一只大象。我们怎么从最开始每个盲人摸到的自己的这一块的面积，能得到最后的组合出这个大象的？那么中间就涉及到这个参数，我们各自的参数乘上我们最开始每个盲人他们摸到自己这一块的内容，他们进行相互的组合，为了让最后能够得到这只大象，我们中间的训练的时候，肯定就要把这个参数进行调整或者最终进行固定，固定之后呢让这个形状呢尽可能接近一头大象，所以这样的话在我们通过大量的数据反复的进行训练之后，我们就能够让我们参数固定下来，固定下来之后呢我们大象就有了。

我们传入的是一个一个的相同点，传出的是一只大象，这些相同点会进行随意的组合，他有可能会符合一只大象也有可能不符合，为什么它最终能得到一只大象，那是因为我们前面训练的特征值和目标值这种数据告诉我们的模型它实质大小，然后再进行这种更新参数过程中就把参数固定下来了，固定下来之后最终能够在下次我们传入新的图片之后它能告诉我们这是或者不是一只大象。

数据量的角度

• 深度学习：数据量多，效果更好

• 机器学习：数据量少，效果不是特别好

深度学习需要大量的训练数据集，会有更高的效果，深度学习训练深度神经网络需要大量的算力，因为其中有更多的参数需要去调整。

深度学习的应用场景

1. 图像识别

   • 物体识别
   • 场景识别
   • 人脸检测跟踪
   • 人脸身份认证

2. 自然语言处理技术

   • 机器翻译
   • 文本识别
   • 聊天对话

3. 语音技术

   • 语音识别

4. 自动驾驶

框架

目前企业中常见的深度学习框架有很多，TensorFlow，Keras，MXNet，PyTorch，CNTK，Theano，Caffe，DeepLearning4，Lasagne，Neon等等，当下最主流的框架当属TensorFlow，Keras，MXNet，PyTorch。

PyTorch是Facebook于2017年1月18日发布的python端的开源的深度学习库，基于Torch。支持动态计算图，提供很好的灵活性。在今年（2018年）五月份的开发者大会上，Facebook宣布实现PyTorch与Caffe2无缝结合的PyTorch1.0版本将马上到来。，PyTorch的使用和python的语法相同，整个操作类似Numpy的操作，并且PyTorch使用的是动态计算，会让代码的调试变的更加简单。

神经网络

人工神经网络

人工神经网络(Artificial Neural Network，ANN)，简称神经网络(Neural Network，NN)或类神经网络，是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型，用于对函数进行估计或近似。

和其他机器学习方法一样，神经网络已经被用于解决各种各样的问题，例如机器视觉和语音识别。这些问题都是很难被传统基于规则的编程所解决的。

神经元

神经元可以说是深度学习中最基本的单位元素，相互连接，组成神经网络, 几乎所有深度学习的网络都是由神经元通过不同的方式组合起来。

在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位; 如果某神经元的电位超过了一个“阈值"，那么它就会被激活，即“兴奋“起来，向其他神经元发送化学物质。

一个神经元到下一个神经元再到下下个神经元它们之间相互连接的，它们之间 有数据或者有信息在他们之间传递，这个传递的过程并不是说他会永远都会往下传下去，而是需要在这个过程中它达到一个阈值，达到阈值之后才会接着用这个神经元把数据再传到下一个神经元里面去。

1943年，McCulloch和 Pilts 将上述情形抽象为上图所示的简单模型，这就是一直沿用至今的 M-P神经元模型。把许多这样的神经元按一定的层次结构连接起来，就得到了神经网络。

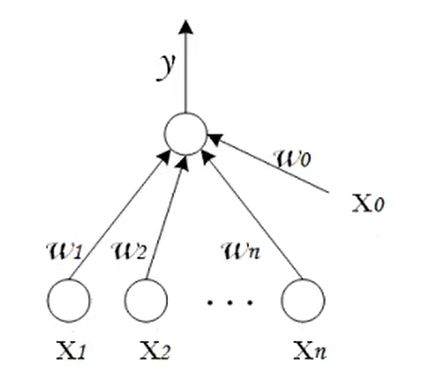
一个简单的神经元如下图所示，

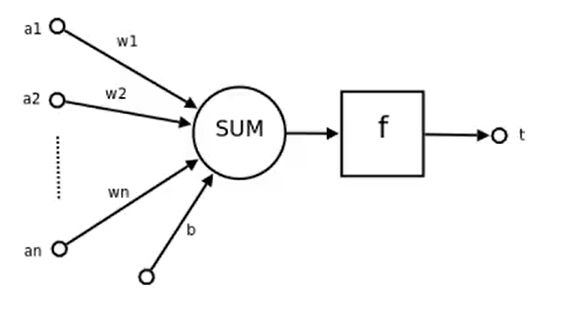
a1、a2…an为各个输入的分量

w1、w2…w3为各个输入分量对应的权重参数

偏置b

f为激活函数，常见的激活函数有tanh，sigmoid，relu

t为神经元的输出

a1、an与各自的参数w1、wn各自相乘，乘上各自的an之后，和b进行一个求和，求和之后会经过一个f函数进行处理，处理之后得到一个output（t）

使用数学公式表示就是：

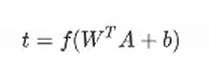
可见，一个神经元的功能是求得输入向量与权向量的内积后，经一个非线性传递函数得到一个标量结果。

总结：人工神经网络就是一个非常大的一个网络，它是用来模拟或者是去对我们的数据进行估计的或者近似的这样一个网络，你可以把它理解为它是一个系统，你可以把它理解为它是一个函数，你可以把它理解为他是一个模型，系统函数模型很多时候都一个意思，都指的是一套操作，这个操作对输入的操作，输入经过这个系统（函数、模型）进行操作之后得到的结果，这就是一个人工神经网络。或者说是人工神经网络模型，只不过这个模型里面他是用的是不同的这种神经元相互连接得到的这种结构，所以我们把这种结构称之为神经网络。

单层的神经网络

单层神经网络是最基本的神经元网络形式，由有限个神经元构成，所有神经元的输入向量都是同一个向量。由于每一个神经元都会产生一个标量结果，所以单层神经元的输出是一个向量，向量的维数等于神经元的数目。

示意图如下：

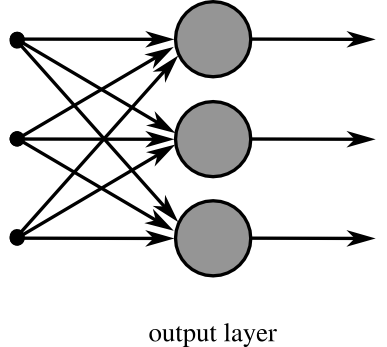
a. 最简单的神经网络的形式

b. 单层的神经网络不是特别常见

两层的神经网络

两层神经网络里面最常见或最基础的这种结构就称之为感知机。感知机指的是两层的神经网络。对于感知机输入有n个神经元, 输出是由一个神经元组成。

感知机

感知机由两层神经网络组成，输入层接收外界输入信号后传递给输出层（输出+1正例，-1反例），输出层是 M-P 神经元。

感知机的作用：

把一个n维向量空间用一个超平面分割成两部分，给定一个输入向量，超平面可以判断出这个向量位于超平面的哪一边，得到输入时正类或者是反类，对应到2维空间就是一条直线把一个平面分为两个部分。

感知机是一个简单的二分类模型，给定阈值，判断数据属于哪一部分

超平面：是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块

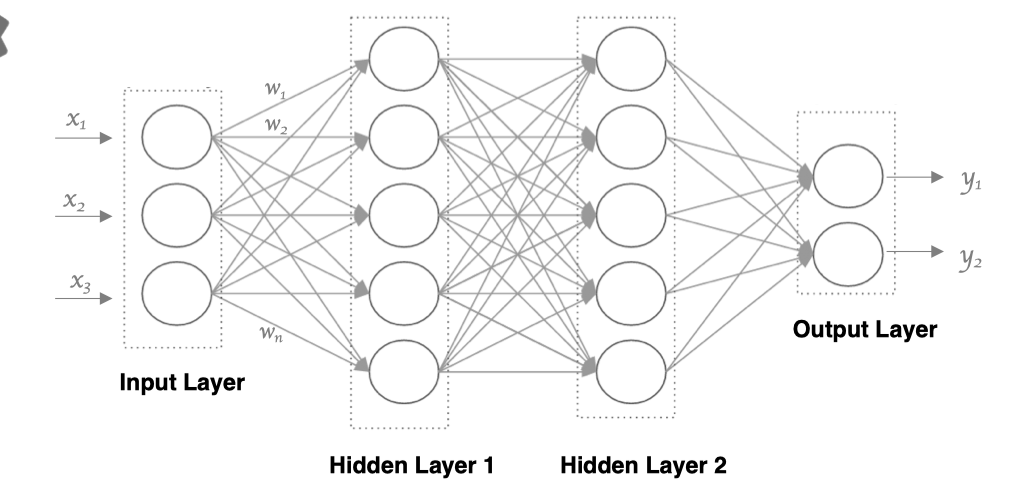
多层神经网络

多层神经网络就是由单层神经网络进行叠加之后得到的，所以就形成了 层 的概念，常见的多层神经网络有如下结构：

• 输入层（Input layer），众多神经元（Neuron）接受大量输入消息。输入的消息称为输入向量。
• 输出层（Output layer），消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。
• 隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（robustness）更显著。

利用神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个强度，示意图如下：

圆圈的地方你可以理解为都是神经元

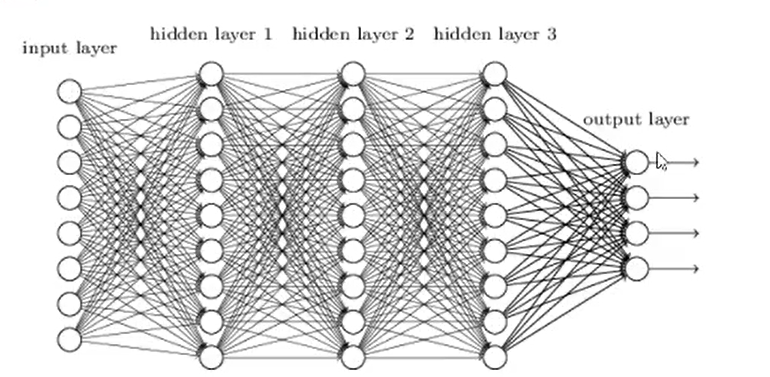
全连接层:当N层的每一个神经元和前一层的每一个神经元都有链接的时候，第N层就是全连接层。就是在进行矩阵乘法，进行特征的变换，就在进行 Y=Wx+b。

思考:假设第N-1层有m个神经元，第N层有n个神经元，当第N层是全连接层的时候，则N-1和N层之间存多少个参数w，这些参数可以如何表示?

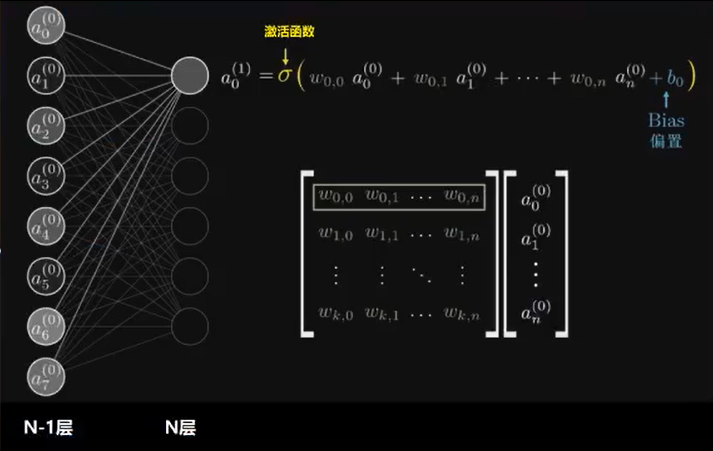
那怎么构建人工神经网络中的神经元呢？

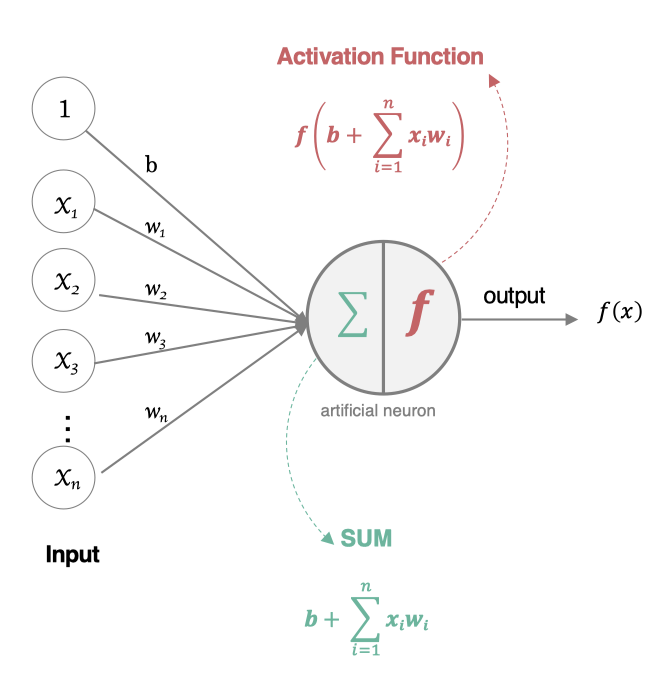
这个流程就像，来源不同树突(树突都会有不同的权重)的信息, 进行的加权计算, 输入到细胞中做加和，再通过激活函数输出细胞值。

1. 所有的输入xi，与相应的权重 wi 相乘并求和

weighted sum= b*1+$x_1$*$w_1$+…+$x_n$*$w_n$=b + ${\sum }_{i=1}^n$$x_i$$w_i$

2. 将求和结果送入到激活函数中，得到最终的输出结果：

f(x)= f ( b+ ${\sum }_{i=1}^n$$x_i$$w_i$ )

激活函数

在前面的神经元的介绍过程中我们提到了激活函数，那么它到底是干什么的呢？

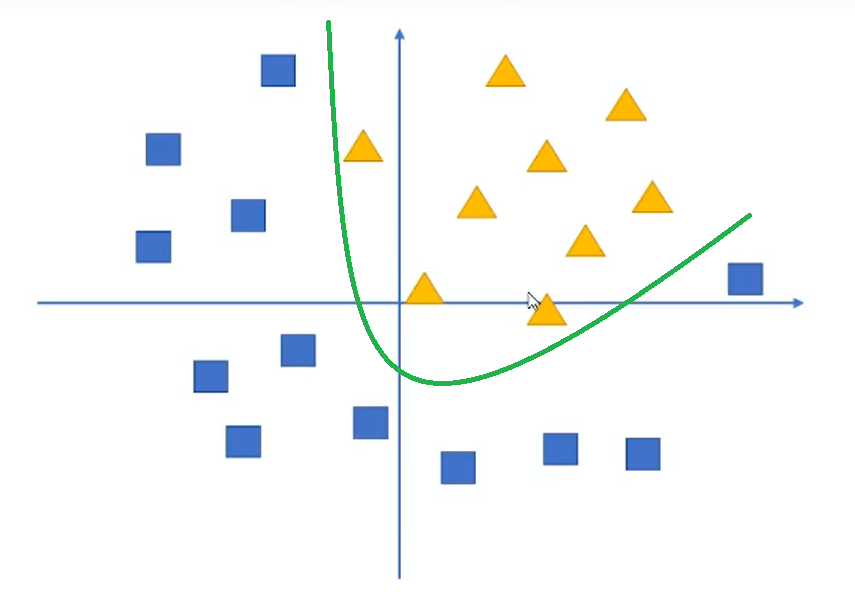
假设我们有这样一组数据，三角形和四边形，需要把他们分为两类

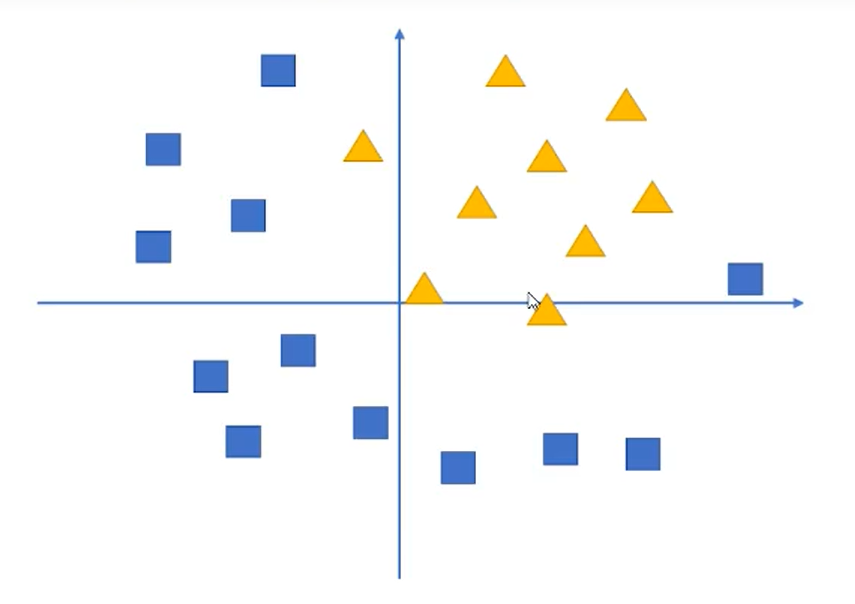
我们画直线是不能把这些进行分类的，我们需要这样一条曲线

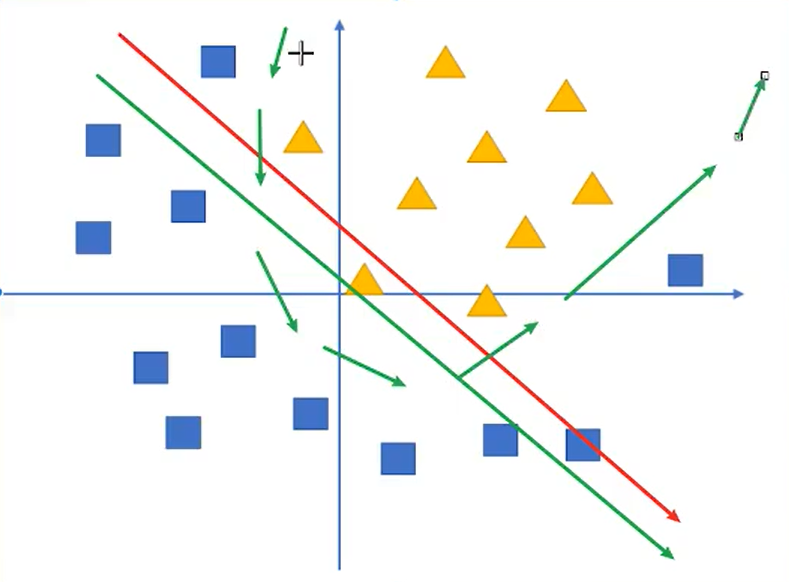
通过不带激活函数的感知机模型我们可以划出一条线, 把平面分割开

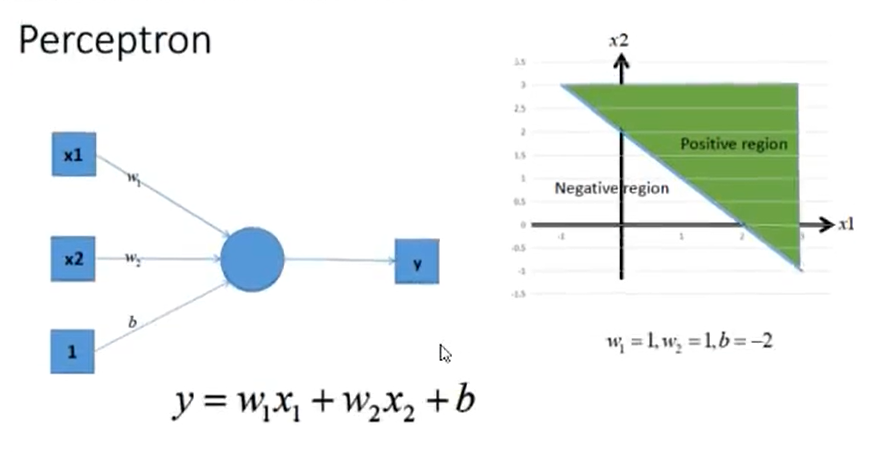
假设我们确定了参数 w 和 b 之后，那么带入需要预测的数据，如果 y>0,我们认为这个点在直线的右边，也就是正类（三角形），否则是在左边（四边形）

但是可以看出，三角形和四边形是没有办法通过直线分开的，那么这个时候该怎么办？

可以考虑使用多层神经网络来进行尝试，比如在前面的感知机模型中再增加一层，如下图：

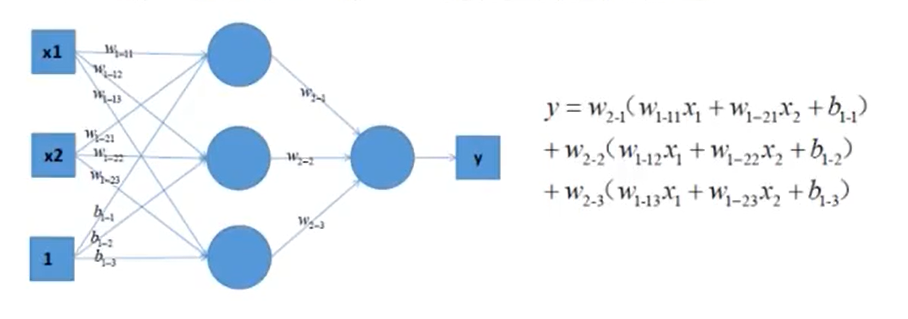
对上图中的等式进行合并，我们可以得到：

y=($w_{1-11}$w${}_{2-1}$+⋯)$x_1$ + ($w_{1-21}$$w_{2-1}$+⋯)$x_2$ + (w${}_{2-1}$+⋯)b${}_{1-1}$

如果说这个 f(x)=y 函数满足两个条件就是线性函数（系统、模型）

• f(x1+x2)= y1+y2
• f(kx1)= ky1

上式括号中的都为w参数，和公式y = $w_1$$x_1$ + $w_2$$x_2$ + b 完全相同，依然只能够绘制出直线。但是可以发现，即使是多层神经网络，相比于前面的感知机，没有任何的改进。

但是如果此时，我们在前面感知机的基础上加上非线性的激活函数之后，输出的结果就不在是一条直线

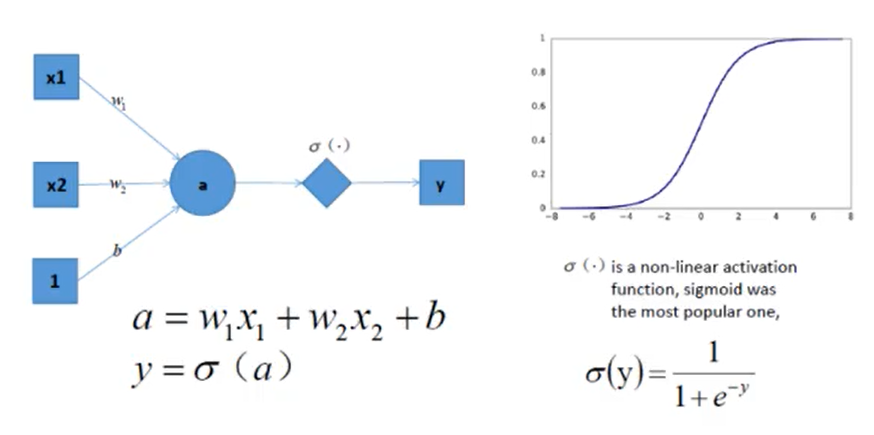
如上图，右边是 sigmoid 函数，对感知机的结果，通过 sigmoid 函数进行处理

如果给定合适的参数 w 和 b，就可以得到合适的曲线，能够完成对最开始问题的非线性分割

所以激活函数很重要的一个作用就是增加模型的非线性分割能力

如果说在感知机或者神经元的基础上，使用了非线性的函数之后，那么输出结果你可以理解为它不再是线性的这样一个结果了。

a施加一个非线性的系统（函数）最终得到一个y，假如前面可能是一条直线，但是经过$\sigma$函数进行处理之后就变成了这样一条曲线了，不再是之前的这样一个直线了。它变成这样一条曲线之后呢，那么对应的我们在这个地方呢可以去寻找一些更合适的参数（w和b），然后呢得到的肯定也会是另外一个曲线，我们只需要不停的去调整，我们最开始的w和b就能够画出来最开始我们所说的这样一条完美的曲线。

如果大家觉得不靠谱, 你可能觉得我施加一个非线性的函数不能够更好的模拟前面的情况的话, 那么前面我们在这里所说的 ( 隐藏层的数目越多的时候, 这个非线性的情况会越显著 ) , 所说的原因就是在于神经元里面添加了非线性激活函数的情况才是这样子。

意思就是说当我们觉得我们要解决这样一个二分的问题，我们使用一个激活函数没办法解决或者使用一个简单的两层神经网络没有办法解决的时候，你可以考虑使用三层四层的这种神经网络结构，在每一层里面对结果都使用这种激活函数进行处理，那么它这个整个模型店非线性的情况就会更加强一些，那么它就会有更多的可能性能够去拟合这些数据，或者有更多的情况能够画出当前刚刚我们所说的这样一条曲线出来，当然它也可能画不出来。它有更大的可能性能够画出这样的一条曲线 ，当然它也有可能画不出来。

前面举的例子，盲人摸象一样，它有可能组合成一头大象，也可能组合不出来，那怎么能够让它真的能够组合成大象呢？那就是我们传入不同的不停的传输更多的数据，让它去调整里面的参数w和b直到它组合出来的是一头象，或者知道它组合出来的曲线是这样子的曲线之后，我们就认为我们的模型已经训练好了。所以这样的话就能够得到一条非常合适的曲线，能够帮助我们进行这样一个分类的问题了。

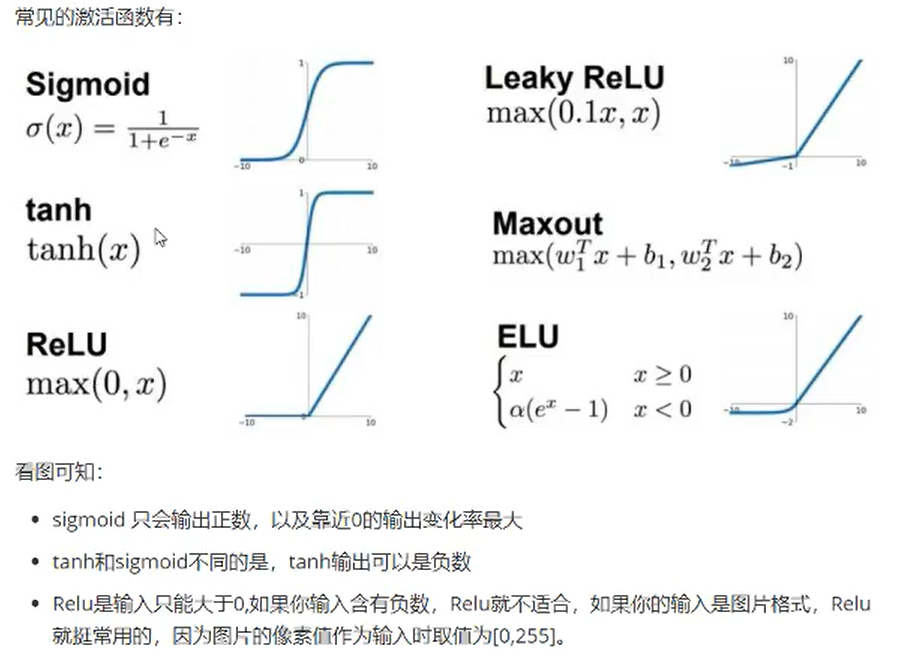
• sigmoid:(0,1)
• tanh:(-1,1)
• relu:max(0,x)
• ELU:$\alpha$(e${}^x$-1)

神经网络示例

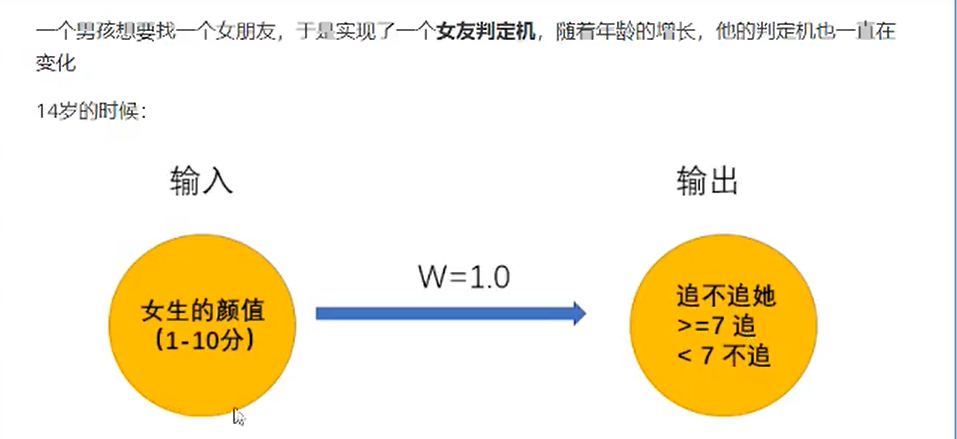
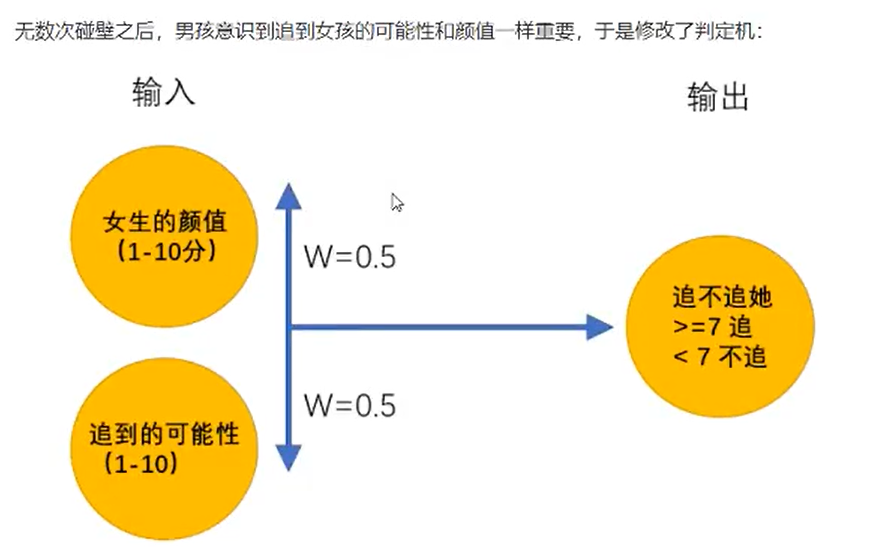
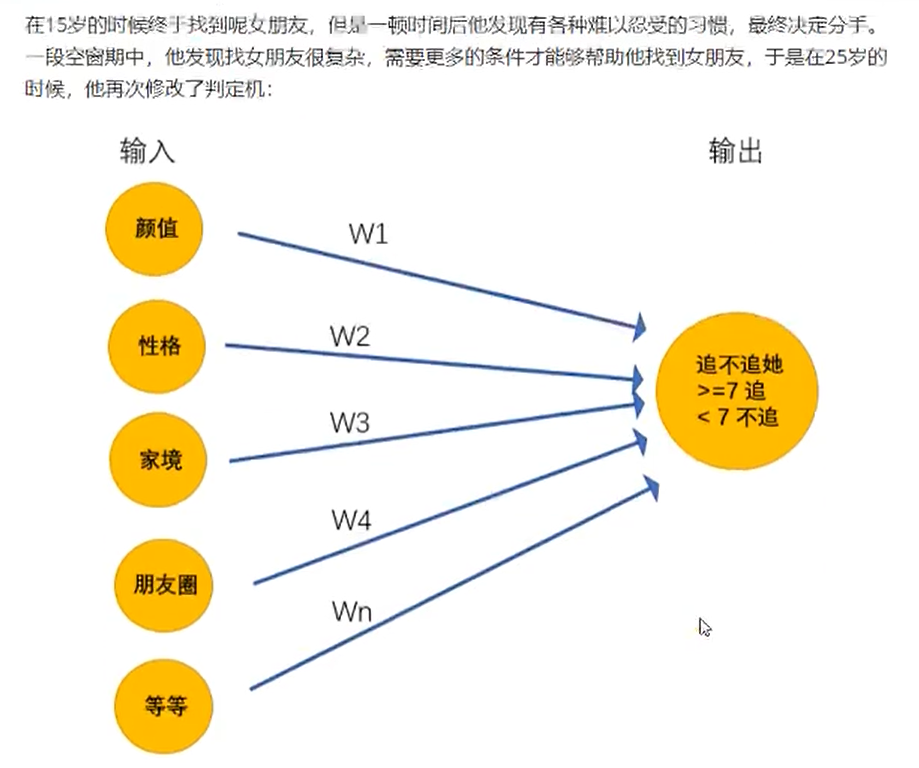
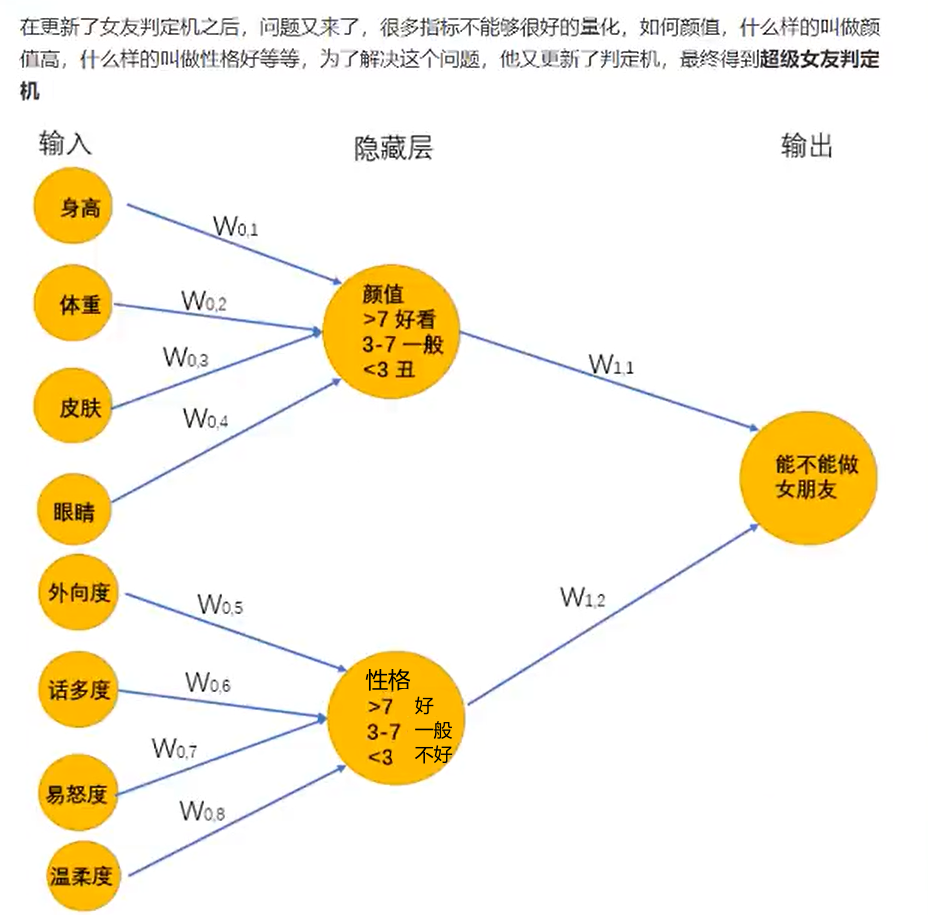
上述的超级女友判定机其实就是神经网络，它能够接受基础的输入，通过隐藏层的线性的和非线性的变化最终的到输出。

通过上面例子，希望大家能够理解深度学习的思想:
输出的最原始、最基本的数据，通过模型来进行特征工程，进行更加高级特征的学习，然后通过传入的数据来确定合适的参数，让模型去更好的拟合数据。

这个过程可以理解为盲人摸象，多个人一起摸，把摸到的结果乘上合适的权重，进行合适的变化，让他和日标值趋近一致。整个过程只需要输入基础的数据，程序自动寻找合适的参数。

总结

激活函数:把原来的数据进行变换

1. 为什么要使用非线性的激活函数

   i. 线性的激活函数或者是不是用激活函数，多层神经网络和两层神经网络没有区别
   ii. 使用非线性的激活函数能够增加模型的非线性分割能力

2. 为什么要使用简单的激活函数(RELU)
   i. RELU方便求导
   ii. sigmoid在取值很大或者很小的时候，导数非常小，会导致参数的更新速度很慢

3. 激活函数的作用:
   i. 增加非线性分割能力
   ii. 增加模型的鲁棒性(或者稳健性, 让模型能够拟合不同的数据)
   iii. 缓解梯度消失
   iv. 加速模型收敛（让模型训练更快一些）