💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:C++入门至进阶
这里将会不定期更新有关C++的内容,希望大家多多点赞关注收藏💖💖
目录
1.什么是优先级队列
优先级队列是一种特殊的队列,其中的元素都被赋予了优先级。元素的优先级决定了它们在队列中的顺序。在优先级队列中,元素按照优先级从高到低的顺序出队列。
优先级队列可以通过不同的数据结构来实现,常用的有二叉堆、二叉搜索树和斐波那契堆等。
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆。
2.仿函数的介绍
仿函数(Functor)是一种重载了函数调用运算符()的类或结构体,它可以像函数一样被调用。通过重载函数调用运算符,仿函数可以实现自定义的操作行为。
仿函数可以像普通函数一样接受参数,并返回结果。它可以用于函数对象的传递、函数指针的替代、算法的灵活性增加等场景。
使用仿函数的步骤如下:
- 定义一个仿函数类或结构体,重载函数调用运算符()。可以根据需要定义构造函数、析构函数和其他成员函数。
- 在代码中创建仿函数对象。仿函数对象可以像函数一样调用,传入参数,并返回结果。
下面是一个示例,演示了使用仿函数实现求平方的功能:
// 定义仿函数类 struct Square { int operator()(int x) const { return x * x; } }; int main() { Square square; // 创建仿函数对象 int result = square(5); // 调用仿函数 // result = 25 return 0; } 在上述示例中,Square 是一个仿函数类,重载了函数调用运算符()。通过创建 Square 对象 square,并像函数一样调用
square(5),可以得到5的平方值25。
通过仿函数,我们可以实现更灵活和自定义的操作行为,并且可以与STL算法等标准库函数配合使用,提高代码的可读性和可维护性。
3.优先级队列使用
| 函数声明 | 接口说明 |
|---|---|
| priority_queue()/priority_queue(first,last) | 构造一个优先级队列 |
| empty( ) | 检测优先级队列是否为空,是返回true,否则返回false |
| top( ) | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
测试代码如下:
#define _CRT_SECURE_NO_WARNINGS 1 #include<iostream> using namespace std; #include<vector> #include <queue> #include <functional> // greater算法的头文件 void TestPriorityQueue() { // 默认情况下,创建的是大堆 vector<int> v = { 3,2,7,6,0,4,1,9,8,5 }; priority_queue<int> q1; //使用范围for入队列 for (auto& e : v) q1.push(e); while (!q1.empty()) { cout << q1.top() << " "; q1.pop(); } cout << endl; // 如果要创建小堆,将第三个模板参数换成greater比较方式 priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end()); while (!q2.empty()) { cout << q2.top() << " "; q2.pop(); } } int main() { TestPriorityQueue(); return 0; } 结果如下: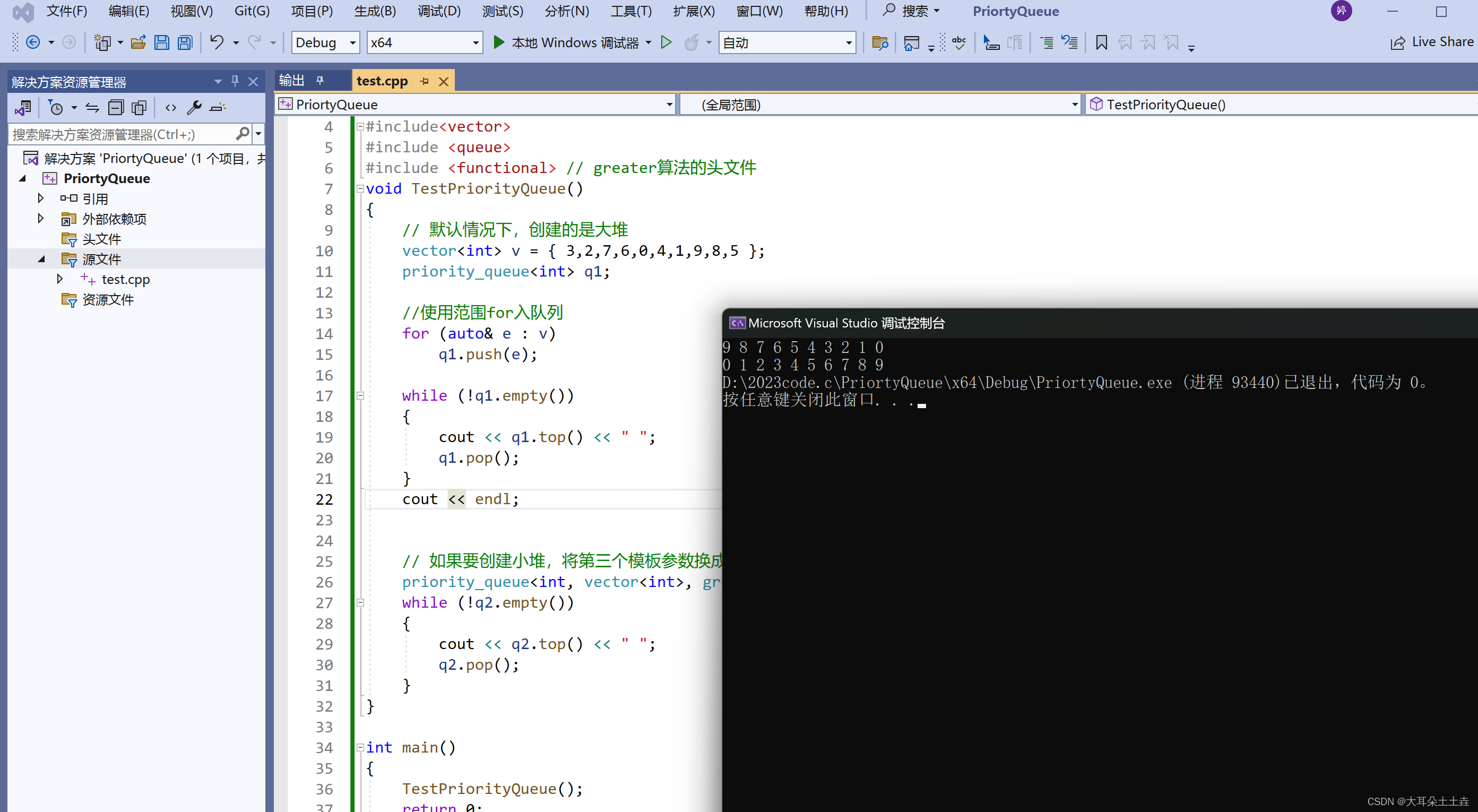
因为实现大堆还是小堆的底层逻辑是不一样的,对应得代码也有些许差异,但为了减少代码的量,提高程序员编程的效率,我们就可以在上述优先级队列的类模板中再传入一个仿函数,对于不同的堆传不同的仿函数类以实现不同的需求;
模板不能直接传入函数,但是可以传类型,可以是自定义类型也可以是内置类型,所以可以传入一个仿函数(它本质是一个类)
4.优先级队列模拟实现
优先级队列模拟实现和队列类似,所不同的是每次插入数据后都会使用算法将队列中的数据调整为一个堆,每次删除也是删除堆顶元素,然后将剩余的元素再次调整为一个堆,这样每次堆顶的元素就是所有数据中优先级最高的那一个了,对于堆算法有疑问的可以点击数据结构——堆的介绍与实现查看
✨堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37}; 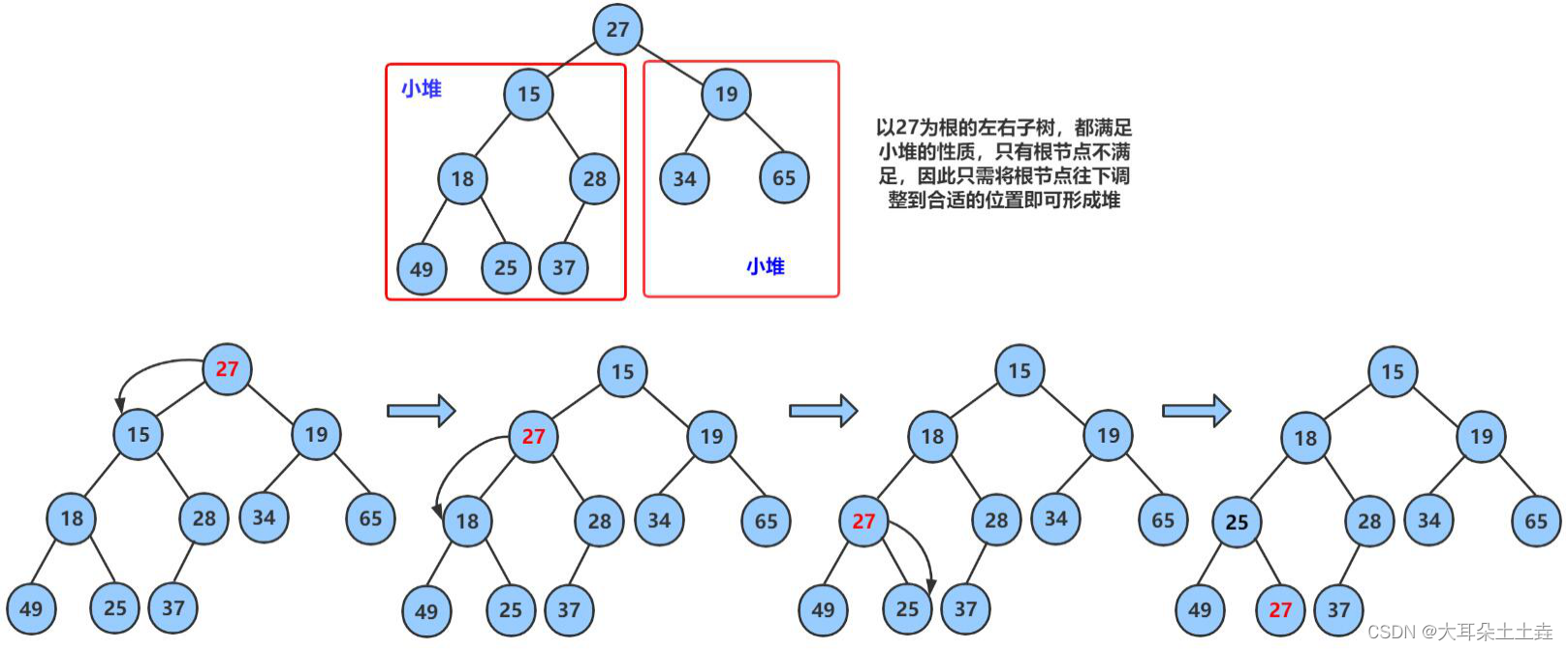
🥳🥳 下面介绍向下调整为小堆;
前提条件——左右子树都是小堆
//堆向下调整算法(小堆) void AdjustDown(HPDataType* a, int n,int parent) { int child = parent * 2 + 1; //向下调整 while (parent < n) { //找到较小的孩子节点 if (child + 1 < n && a[child] > a[child + 1]) { child++; } if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = child * 2 + 1; } else break; } } 因为要调整为小堆,所以要找到孩子中较小的一个进行比较;
如果父节点小于较小的孩子节点则直接break不需要调整,因为向下调整的前提条件是——左右子树都是小堆。
调整前:
调整后:
所以我们就可以利用堆向下调整算法来将堆顶元素与最后一个元素交换后,删除交换后最后一个元素,保证除了交换后堆顶元素外,左右子树都是一个堆,然后利用堆向下调整算法将整个二叉树调整为一个堆
此外堆向下调整算法还可以将一串数据调整为一个堆: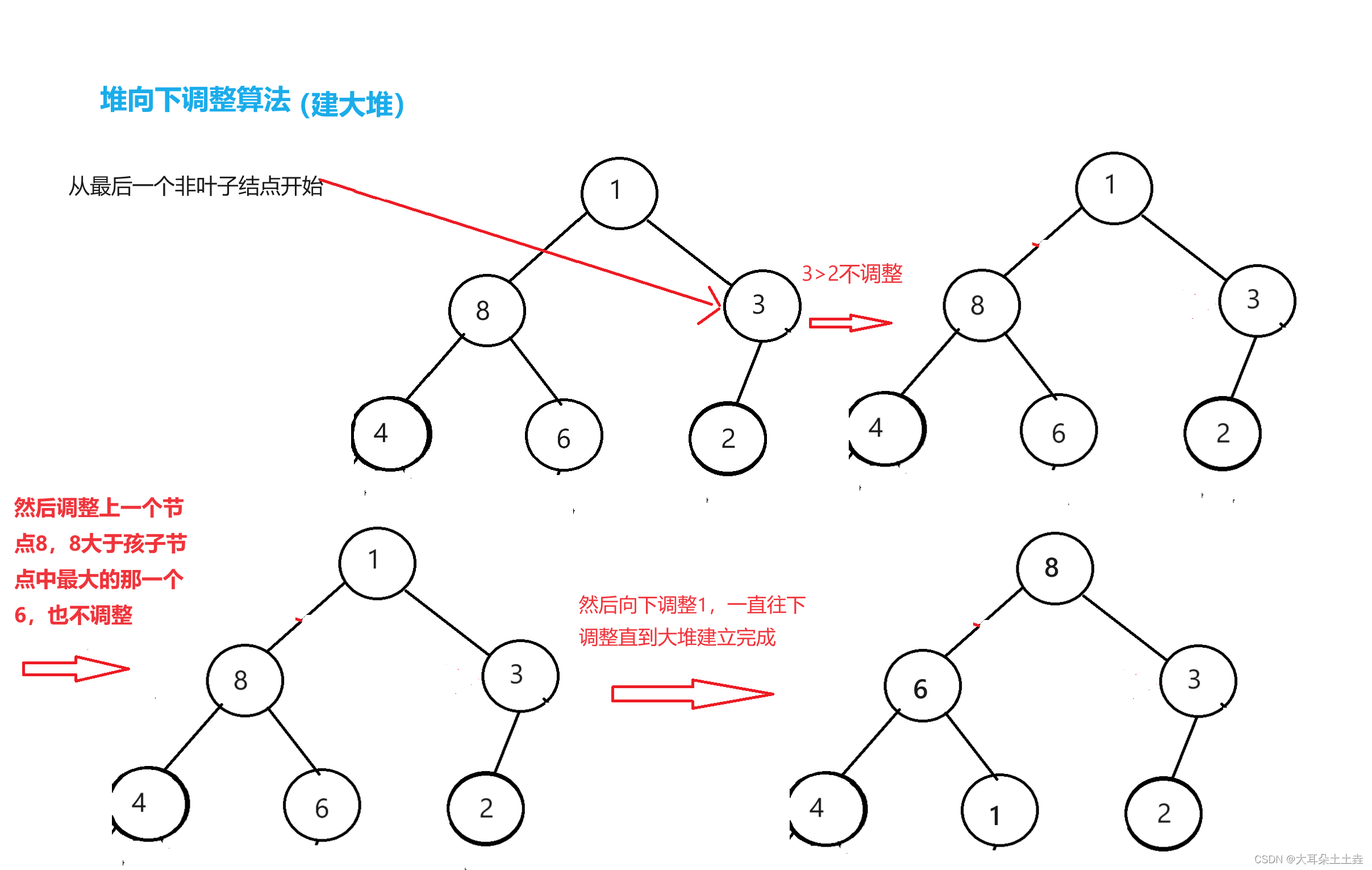
当然堆向上调整算法也可以实现,只不过它的时间复杂度没有堆向下调整算法好,所以我们选择使用堆向下调整算法构建堆
✨堆向上调整算法
我们知道堆的父节点必须都大于或小于子节点,那么往一个堆中插入元素是没办法保证大于或小于其父节点的,所以我们插入之后需要调整这个二叉树来保证堆;
这里就要用到堆向上调整算法了;注意下面是小堆的调整
堆向上调整算法
//向上调整 void AdjustUp(HPDataType* a,int child) { //找到双亲节点 int parent = (child - 1) / 2; //向上调整 while (child > 0) { if (a[parent] > a[child]) { Swap(&a[parent], &a[child]); child = parent; parent = (child - 1) / 2; } else break; } } 堆向上调整类似于向下调整也有大堆小堆之分,大家可以依照堆的向下调整自己试试看写一下大堆的向上调整
✨仿函数
有了堆向下调整算法来删除堆顶元素和建堆,以及堆向上调整算法尾插元素,我们就可以实现优先级队列了🥳🥳
但是优先级队列能否按照我们需要选择大堆还是小堆呢?
这就需要利用我们之前学习的仿函数,传入一个类模板class Compare,当我们想要建小堆的时候就选择相应的类即可
//实现大堆 template<class T> struct Less { bool operator()(const T& x, const T& y) { return x < y; } }; //实现小堆 template<class T> struct Greater { bool operator()(const T& x, const T& y) { return x > y; } }; 注意这里类的名字是我们自己取的,为了和STL库里面的命名保持一致,我们使用Less建立大堆,Greater建立小堆,因为建大堆还是小堆关键就在于父节点与孩子节点比较是大于还是小于,所以我们将所有比较的地方都使用仿函数,这样就可以按照我们希望的方式来比较,如果希望是大堆,就按Less中的<来比较;小堆就按照Greater中的>来比较
这样就可以将上述仿函数传给优先级队列了:
//优先级队列的模拟实现 template<class T, class Container = vector<T>,class Compare = Less<T>>//默认是大堆 class priority_queue {} ✨优先级队列模拟实现
#pragma once #include<iostream> using namespace std; #include<vector> #include <queue> #include <functional> // greater算法的头文件 namespace tutu //防止命名冲突 { template<class T> struct Less { bool operator()(const T& x, const T& y) { return x < y; } }; template<class T> struct Greater { bool operator()(const T& x, const T& y) { return x > y; } }; //优先级队列的模拟实现 template<class T, class Container = vector<T>,class Compare = Less<T>> class priority_queue { public: //强制生成默认构造函数 priority_queue() = default; //迭代器构造 template<class InputIterator> priority_queue(InputIterator begin, InputIterator end) { //入队列 while (begin != end) { _c.push_back(*begin); begin++; } //调整数据为堆 for (int i = ((int)_c.size() - 1-1)/2; i >= 0; i--) { Adjust_Down(i); } } //initializer_list构造 priority_queue(initializer_list<T> il) { for (const auto& e : il) { _c.push_back(e); } //调整数据为堆 for (int i = ((int)_c.size() - 1-1)/2; i >= 0; i--) { Adjust_Down(i); } } //向上调整算法 void Adjust_Up(int child) { int parent = (child - 1) / 2; while (child > 0) { if (_comp(_c[parent] , _c[child])) { swap(_c[parent], _c[child]); child = parent; parent = (child - 1) / 2; } else { break; } } } //插入元素 void push(const T& val) { _c.push_back(val); Adjust_Up(_c.size() - 1); } //向下调整算法 void Adjust_Down(int parent) { int child = parent * 2 + 1; while (parent< _c.size()) { //找更大的孩子节点 if (child + 1 < _c.size() && _comp(_c[child ] , _c[child+1])) { child++; } if (child<_c.size() && _comp(_c[parent] , _c[child])) { swap(_c[parent], _c[child]); parent = child; child = parent * 2 + 1; } else { break; } } } //删除堆顶元素 void pop() { swap(_c[0], _c[_c.size() - 1]); _c.pop_back(); Adjust_Down(0); } //取堆顶元素 T& top() { return _c[0]; } const T& top()const { return _c[0]; } size_t size() const { return _c.size(); } bool empty() const { return _c.empty(); } private: Container _c;//底层容器 Compare _comp; //比较方式 }; } ✨测试代码
//测试代码 void test1() { priority_queue<int> p; p.push(1); p.push(8); p.push(3); p.push(4); p.push(6); p.push(2); while (!p.empty()) { cout << p.top() << " "; p.pop(); } } //迭代器构造测试 void test2() { vector<int> v{ 1, 7, 8, 4, 5, 9, 2, 3, 6 }; priority_queue<int> p(v.begin(), v.end()); while (!p.empty()) { cout << p.top() << " "; p.pop(); } } //initializer_list构造测试代码 void test3() { priority_queue<int> p = { 1,4,7,5,3,9,2,6,8 }; while (!p.empty()) { cout << p.top() << " "; p.pop(); } } 我们使用test1测试,结果如下:
发现每次取的都是堆顶的元素(也就是数据中优先级最高的那一个)
5.结语
前面我们学习过栈和队列,优先级队列和它们类似,所不同的是每次插入数据都需要使用堆算法来调整建堆,删除堆顶数据后也需要进行建堆,这样每次堆顶元素都是优先级最高的那个元素,以上就是优先级队列的所有内容啦~ 完结撒花 ~🥳🎉🎉