LeetCode 3067.在带权树网络中统计可连接服务器对数目：枚举根_业界新闻

发布时间:2024-07-13 17:14

阅读量:3

【LetMeFly】3067.在带权树网络中统计可连接服务器对数目：枚举根

力扣题目链接：https://leetcode.cn/problems/count-pairs-of-connectable-servers-in-a-weighted-tree-network/

给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [a_i, b_i, weight_i] 表示节点 a_i 和 b_i 之间有一条双向边，边的权值为 weight_i 。再给你一个整数 signalSpeed 。

如果两个服务器 a ，b 和 c 满足以下条件，那么我们称服务器 a 和 b 是通过服务器 c 可连接的 ：

a < b ，a != c 且 b != c 。
从 c 到 a 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的数目。

示例 1：

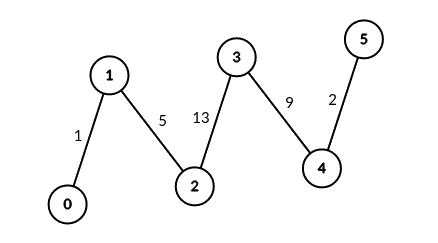
输入：edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1 输出：[0,4,6,6,4,0] 解释：由于 signalSpeed 等于 1 ，count[c] 等于所有从 c 开始且没有公共边的路径对数目。 在输入图中，count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。

示例 2：

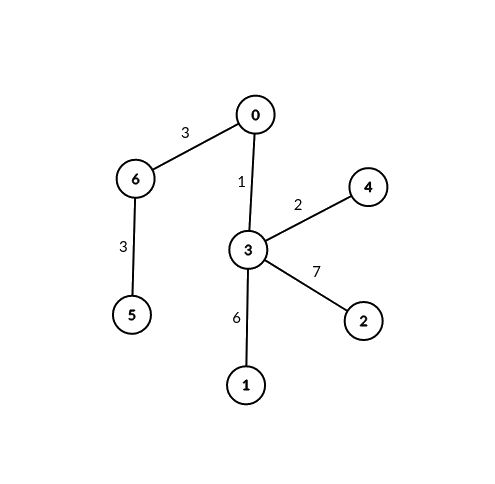
输入：edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3 输出：[2,0,0,0,0,0,2] 解释：通过服务器 0 ，有 2 个可连接服务器对(4, 5) 和 (4, 6) 。 通过服务器 6 ，有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。 所有服务器对都必须通过服务器 0 或 6 才可连接，所以其他服务器对应的可连接服务器对数目都为 0 。

提示：

2 <= n <= 1000
edges.length == n - 1
edges[i].length == 3
0 <= a_i, b_i < n
edges[i] = [a_i, b_i, weight_i]
1 <= weight_i <= 10⁶
1 <= signalSpeed <= 10⁶
输入保证 edges 构成一棵合法的树。

解题方法：枚举根

枚举每个节点作为c，以c为根，求每个“子树”中有多少节点离c的距离是signalSpeed的总个数（可以通过DFS求出）。

    c    / \    *  ***   **

假设所有子树中符合要求的节点数分别为[4, 5, 8]，则以c为根的总对数为4 * 5 + 4 * 8 + 5 * 8（两两相乘）。

时间复杂度 $O(n^2)$
空间复杂度 $O (n)$

AC代码

C++

class Solution { private:     vector<vector<pair<int, int>>> graph;     int signalSpeed;      int dfs(int from, int to, int cntDistance) {         int ans = cntDistance % signalSpeed == 0;         for (auto [nextNode, nextDistance] : graph[to]) {             if (nextNode == from) {                 continue;             }             ans += dfs(to, nextNode, cntDistance + nextDistance);         }         return ans;     } public:     vector<int> countPairsOfConnectableServers(vector<vector<int>>& edges, int signalSpeed) {         // init         graph.resize(edges.size() + 1);         this->signalSpeed = signalSpeed;         for (vector<int>& edge : edges) {             graph[edge[0]].push_back({edge[1], edge[2]});             graph[edge[1]].push_back({edge[0], edge[2]});         }         // calculate         vector<int> ans(edges.size() + 1);         for (int c = 0; c < ans.size(); c++) {             vector<int> ab;  // c为根的每个边上有多少ab节点             for (auto [to, distance] : graph[c]) {                 ab.push_back(dfs(c, to, distance));             }             for (int i = 0; i < ab.size(); i++) {                 for (int j = i + 1; j < ab.size(); j++) {                     ans[c] += ab[i] * ab[j];                 }             }         }         return ans;     } };

Python

# from typing import List  class Solution:     def dfs(self, from_: int, to: int, cntDistance: int) -> int:         ans = 0 if cntDistance % self.signalSpeed else 1         for nextNode, nextDistance in self.graph[to]:             if nextNode == from_:                 continue             ans += self.dfs(to, nextNode, cntDistance + nextDistance)         return ans      def countPairsOfConnectableServers(self, edges: List[List[int]], signalSpeed: int) -> List[int]:         # init         self.signalSpeed = signalSpeed         graph = [[] for _ in range(len(edges) + 1)]         for x, y, d in edges:             graph[x].append((y, d))             graph[y].append((x, d))         self.graph = graph         # calculate         ans = [0] * (len(edges) + 1)         for c in range(len(ans)):             ab = []             for to, distance in graph[c]:                 ab.append(self.dfs(c, to, distance))             for i in range(len(ab)):                 for j in range(i + 1, len(ab)):                     ans[c] += ab[i] * ab[j]         return ans